Consistent incompatible systems of linear equations. Solving systems of linear equations

The system is called joint, or solvable, if it has at least one solution. The system is called incompatible, or unsolvable, if it has no solutions.

Definite, indefinite SLAU.

If a SLAE has a solution, and a unique one at that, then it is called certain and if the solution is not unique, then uncertain.

MATRIX EQUATIONS

Matrices make it possible to briefly write down the system linear equations. Let a system of 3 equations with three unknowns be given:

Consider the system matrix and matrices columns of unknown and free terms

Let's find the work

those. as a result of the product, we obtain the left-hand sides of the equations of this system. Then using the definition of matrix equality this system can be written in the form

or shorter A∙X=B.

Here are the matrices A And B are known, and the matrix X unknown. It is necessary to find it, because... its elements are the solution to this system. This equation is called matrix equation.

Let the matrix determinant be different from zero | A| ≠ 0. Then matrix equation is solved as follows. Multiply both sides of the equation on the left by the matrix A-1, inverse of the matrix A: . Because the A -1 A = E And E∙X = X, then we obtain a solution to the matrix equation in the form X = A -1 B .

Note that since the inverse matrix can only be found for square matrices, the matrix method can only solve those systems in which the number of equations coincides with the number of unknowns.

Cramer's formulas

Cramer's method consists in sequentially finding main determinant of the system, i.e. determinant of matrix A: D = det (a i j) and n auxiliary determinants D i (i= ), which are obtained from the determinant D by replacing the i-th column with a column of free terms.

Cramer's formulas look like: D × x i = D i (i = ).

From this follows Cramer's rule, which gives an exhaustive answer to the question of the compatibility of a system: if the main determinant of the system is different from zero, then the system has only decision, determined by the formulas: x i = D i / D.

If the main determinant of the system D and all auxiliary determinants D i = 0 (i= ), then the system has an infinite number of solutions. If the main determinant of the system D = 0, and at least one auxiliary determinant is different from zero, then the system is inconsistent.

Theorem (Cramer's rule): If the determinant of the system Δ ≠ 0, then the system under consideration has one and only one solution, and

Proof: So, consider a system of 3 equations with three unknowns. Let's multiply the 1st equation of the system by algebraic complement A 11 element a 11, 2nd equation – on A 21 and 3rd – on A 31:

Let's add these equations:

Let's look at each of the brackets and the right side of this equation. By the theorem on the expansion of the determinant into elements of the 1st column.

Similarly, it can be shown that and .

Finally, it is easy to notice that

Thus, we obtain the equality: . Hence, .

The equalities and are derived similarly, from which the statement of the theorem follows.

Kronecker-Capelli theorem.

A system of linear equations is consistent if and only if the rank of the system matrix is ​​equal to the rank of the extended matrix.

Proof: It breaks down into two stages.

1. Let the system have a solution. Let's show that.

Let a set of numbers is a solution to the system. Let us denote by the th column of the matrix, . Then, that is, the column of dummy terms is a linear combination of the columns of the matrix. Let . Let's pretend that . Then by . Let's choose in basic minor. He has order. The column of free terms must pass through this minor, otherwise it will be the basis minor of the matrix. The column of dummy terms in the minor is a linear combination of the columns of the matrix. Due to the properties of the determinant, where is the determinant that is obtained from the minor by replacing the column of free terms with the column . If the column passed through the minor M, then in , there will be two identical columns and, therefore, . If the column did not pass through the minor, then it will differ from the minor of order r+1 of the matrix only in the order of the columns. Since, then. Thus, which contradicts the definition of a basis minor. This means that the assumption that , is incorrect.

2. Let . Let us show that the system has a solution. Since , then the basis minor of the matrix is ​​the basis minor of the matrix. Let the columns pass through the minor . Then, by the theorem on the basis minor in a matrix, the column of free terms is a linear combination of the indicated columns:

(1)

Let us put , , , , and take the remaining unknowns equal to zero. Then with these values ​​we get

By virtue of equality (1) . The last equality means that the set of numbers is a solution to the system. The existence of a solution has been proven.

In the system discussed above , and the system is cooperative. In the system , , and the system is inconsistent.

Note: Although the Kronecker-Capelli theorem makes it possible to determine whether a system is consistent, it is used quite rarely, mainly in theoretical research. The reason is that the calculations performed to find the rank of a matrix are essentially the same as the calculations performed to find the solution to the system. Therefore, usually, instead of finding and , they look for a solution to the system. If we can find it, we find out that the system is consistent and at the same time obtain its solution. If a solution cannot be found, then we conclude that the system is inconsistent.

Algorithm for finding solutions to an arbitrary system of linear equations (Gauss method)

Let a system of linear equations with unknowns be given. It is required to find its general solution, if it is compatible, or to establish its incompatibility. The method that will be presented in this section is close to the method of calculating the determinant and to the method of finding the rank of a matrix. The proposed algorithm is called Gaussian method or by the method of sequential exclusion of unknowns.

Let us write down the extended matrix of the system

Let us call the following operations with matrices elementary operations:

1. rearrangement of lines;

2. multiplying a string by a number other than zero;

3. adding a string to another string multiplied by a number.

Note that when solving a system of equations, unlike calculating the determinant and finding the rank, you cannot operate with columns. If a system of equations is restored from the matrix obtained by performing an elementary operation, then the new system will be equivalent to the original one.

The goal of the algorithm is to, by applying a sequence of elementary operations to the matrix, ensure that each row, except perhaps the first, begins with zeros, and the number of zeros before the first non-zero element in each subsequent row is greater than in the previous one.

The algorithm step is as follows. Find the first non-zero column in the matrix. Let this be a column with number . We find a non-zero element in it and swap the line with this element with the first line. In order not to add additional notation, we will assume that such a change of rows in the matrix has already been made, that is. Then to the second line we add the first, multiplied by the number, to the third line we add the first, multiplied by the number, etc. As a result, we get the matrix

(The leading zero columns are usually missing.)

If the matrix contains a row with number k, in which all elements are equal to zero, and , then we stop the execution of the algorithm and conclude that the system is inconsistent. Indeed, restoring the system of equations from the extended matrix, we obtain that the th equation will have the form

No set of numbers satisfies this equation. .

The matrix can be written in the form

In relation to the matrix, we perform the described step of the algorithm. We get the matrix

Where , . This matrix can again be written as

and again apply the algorithm step described above to the matrix.

The process stops if, after performing the next step, the new reduced matrix consists of only zeros or if all rows are exhausted. Note that the conclusion that the system is incompatible could have stopped the process earlier.

If we had not reduced the matrix, we would have ended up with a matrix of the form

Next, the so-called reverse of the Gaussian method is performed. Using the matrix, we compose a system of equations. On the left side we leave unknowns with numbers corresponding to the first non-zero elements in each line, that is. Notice, that . We move the remaining unknowns to the right side. Considering the unknowns on the right side to be certain fixed quantities, it is easy to express the unknowns on the left side through them.

Now, by assigning arbitrary values ​​to the unknowns on the right side and calculating the values ​​of the variables on the left side, we will find various solutions to the original system Ax=b. To write down the general solution, you need to denote the unknowns on the right side in some order by letters , including those unknowns that are not explicitly written out on the right side due to zero coefficients, and then the column of unknowns can be written as a column, where each element is a linear combination of arbitrary quantities (in particular, just an arbitrary value ). This entry will be the general solution of the system.

If the system was homogeneous, then we obtain the general solution of the homogeneous system. The coefficients for , taken in each element of the general solution column, will form the first solution from the fundamental system of solutions, the coefficients for - the second solution, etc.

Method 2: The fundamental system of solutions of a homogeneous system can be obtained in another way. To do this, one variable moved to the right side must be assigned the value 1, and the rest - zeros. Having calculated the values ​​of the variables on the left side, we obtain one solution from the fundamental system. By assigning the value 1 to another variable on the right-hand side and zeros to the rest, we obtain the second solution from the fundamental system, etc.

Definition: the system is called jointly th if it has at least one solution, and inconsistent - otherwise, that is, in the case when the system has no solutions. The question of whether a system has a solution or not is connected not only with the ratio of the number of equations and the number of unknowns. For example, a system of three equations with two unknowns

has a solution, and even has infinitely many solutions, but a system of two equations with three unknowns.

……. … ……

A m 1 x 1 + … + a mn x n = 0

This system is always consistent since it has a trivial solution x 1 =...=x n =0

For the existence of nontrivial solutions it is necessary and sufficient to satisfy

conditions r = r(A)< n , что равносильно условию det(A)=0, когда матрица А – квадратная.

Th The set of solutions of the SLAE forms a linear space of dimension (n-r). This means that the product of its solution by a number, as well as the sum and linear combination of a finite number of its solutions, are solutions to this system. The linear solution space of any SLAE is a subspace of the space Rn.

Any set of (n-r) linearly independent solutions of a SLAE (which is a basis in the solution space) is called fundamental set of solutions (FSR).

Let x 1 ,…, x r be the basic unknowns, x r +1 ,…, x n – free unknowns. Let us give the free variables the following values ​​in turn:

……. … ……

A m 1 x 1 + … + a mn x n = 0

Forms a linear space S (solution space), which is a subspace in R n (n is the number of unknowns), and dims=k=n-r, where r is the rank of the system. The basis in the solution space(x (1) ,…, x (k)) is called the fundamental solution system, and the general solution has the form:

X=c 1 x (1) + … + c k x (k) , c (1) ,…, c (k) ? R

Section 5. ELEMENTS OF LINEAR ALGEBRA

Systems of linear equations

Basic Concepts

A system of linear algebraic equations, containing T equations and P unknowns is called a system of the form

where are the numbers A ij , i=
, j= are called coefficients systems, numbers b i - free members. Numbers to be found X P .

It is convenient to write such a system in a compact matrix form
.

Here A is the matrix of system coefficients, called main matrix:

,

–column vector of unknowns X j , – column vector of free terms b i .

Expanded matrix of the system called a matrix system supplemented by a column of free members

.

By decision system is called P unknown values X 1 =c 1 , X 2 =c 2 , ..., X P =c P , upon substitution, all equations of the system turn into true equalities. Any solution to the system can be written as a column matrix .

The system of equations is called joint, if it has at least one solution, and non-joint, if it does not have a single solution.

The joint system is called certain, if it has a unique solution, and uncertain, if it has more than one solution. In the latter case, each of its solutions is called private solution systems. The set of all particular solutions is called general solution.

Solve the system – this means finding out whether it is compatible or not compatible. If the system is consistent, then find its general solution.

The two systems are called equivalent(equivalent) if they have the same general solution. In other words, systems are equivalent if every solution of one of them is a solution of the other, and vice versa.

Equivalent systems are obtained, in particular, when elementary transformations system, provided that the transformations are performed only on the rows of the matrix.

The system of linear equations is called homogeneous, if all free terms are equal to zero:

A homogeneous system is always consistent, since X 1 =x 2 =…=x P =0 is a solution to the system. This solution is called zero or trivial.

Solving systems of linear equations

Let an arbitrary system be given T linear equations with P unknown

Theorem 1(Kronecker-Capelli). A system of linear algebraic equations is consistent if and only if the rank of the extended matrix is ​​equal to the rank of the main matrix.

Theorem 2. If the rank of a joint system is equal to the number of unknowns, then the system has a unique solution.

Theorem 3. If the rank of a consistent system is less than the number of unknowns, then the system has an infinite number of solutions.

EXAMPLE Examine the system for compatibility

Solution.
,r(A)=1;
, r()=2,
.

Thus, r(A) r(), therefore the system is inconsistent.

Solving non-degenerate systems of linear equations. Cramer's formulas

Let the system be given P linear equations with P unknown

or in matrix form A∙X=B.

The main matrix A of such a system is square. The determinant of this matrix is ​​called determinant of the system. If the determinant of the system is different from zero, then the system is called non-degenerate.

Let's find a solution to this system of equations in the case of ∆0. multiplying both sides of the equation A∙X=B on the left by the matrix A  1, we obtain A  1 ∙ A∙X= A  1 ∙B. Since A  1 ∙ A=E and E∙X=X, then X= A  1 ∙ B. This method of solving the system is called matrix.

From the matrix method it follows Cramer's formulas
, where ∆ is the determinant of the main matrix of the system, and ∆ i is the determinant obtained from the determinant ∆ by replacing i The th column of coefficients is a column of free terms.

EXAMPLE Solve the system

Solution.
, 70,
,
. Means, X 1 =, X 2 =
.

Solving systems of linear equations using the Gauss method

The Gaussian method consists of sequential elimination of unknowns.

Let a system of equations be given

The Gaussian solution process consists of two stages. At the first stage (direct motion), the system is brought to stepwise(in particular, triangular) mind.

Where k≤ n, a ii  0, i= . Odds A ii are called main elements of the system.

At the second stage (reverse) there is a sequential determination of the unknowns from this stepwise system.

Notes:

If the step system turns out to be triangular, i.e. k= n, then the original system has a unique solution. From the last equation we find X P , from the penultimate equation we find X P  1 , Then, going up the system, we will find all the other unknowns.

In practice, it is more convenient to work with the extended matrix of the system, performing all the elementary transformations on its rows. It is convenient that the coefficient A 11 was equal to 1 (rearrange the equations or divide by A 11 1).

EXAMPLE Solve the system using the Gaussian method

Solution. As a result of elementary transformations over the extended matrix of the system

~
~
~

~

the original system was reduced to a stepwise one:

Therefore, the general solution of the system is: x 2 =5 x 4  13 x 3  3; x 1 =5 x 4  8 x 3  1.

If we put, for example, X 3 =x 4 =0, then we will find one of the particular solutions of this system X 1 =  1, x 2 =  3, x 3 =0, x 4 =0.

Systems of homogeneous linear equations

Let a system of linear homogeneous equations be given

It is obvious that a homogeneous system is always consistent; it has a zero (trivial) solution.

Theorem 4. In order for a system of homogeneous equations to have a non-zero solution, it is necessary and sufficient that the rank of its main matrix be less than the number of unknowns, i.e. r< n.

Theorem 5. In order for a homogeneous system P linear equations with P unknowns had a non-zero solution, it is necessary and sufficient that the determinant of its main matrix be equal to zero, i.e. ∆=0.

If the system has non-zero solutions, then ∆=0.

EXAMPLE Solve the system

Solution.
,r(A)=2
, n=3. Because r< n, then the system has an infinite number of solutions.

,
. That is, X 1 ==2x 3 , X 2 ==3x 3 - common decision.

Putting X 3 =0, we get one particular solution: X 1 =0, x 2 =0, x 3 =0. Putting X 3 =1, we get the second particular solution: X 1 =2, x 2 =3, x 3 =1 etc.

Questions for control

What is a system of linear algebraic equations?

Explain the following concepts: coefficient, dummy term, basic and extended matrices.

What are the types of systems of linear equations? State the Kronker-Capelli theorem (on the compatibility of a system of linear equations).

List and explain methods for solving systems of linear equations.

Definition. System m equations with n unknowns in general view is written as follows:

Where a ij are the coefficients, and b i– permanent.

The solutions of the system are n numbers that, when substituted into the system, turn each of its equations into an identity.

Definition. If a system has at least one solution, then it is called joint. If a system does not have a single solution, then it is called inconsistent.

Definition. A system is called determinate if it has only one solution and indefinite if it has more than one.

Definition. For a system of linear equations the matrix

A = is called the matrix of the system, and the matrix

A * = called the extended matrix of the system

Definition. If b 1 , b 2 , …,b m = 0, then the system is called homogeneous. Comment. A homogeneous system is always consistent, because always has a zero solution.

Elementary transformations of systems.

1. Adding to both sides of one equation the corresponding parts of the other, multiplied by the same number, not equal to zero.

2. Rearranging equations.

3. Removing from the system equations that are identities for all X.

Cramer's formulas.

This method is also applicable only in the case of systems of linear equations, where the number of variables coincides with the number of equations.

Theorem. System of n equations with n unknowns

if the determinant of the system matrix is ​​not equal to zero, then the system has a unique solution and this solution is found using the formulas: x i = Where D = det A, A D i is the determinant of the matrix obtained from the system matrix by replacing the column i column of free members b i.

D i =

Example. Find the solution to the system of equations:

D = = 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30;

D 1 = = (28 – 48) – (42 – 32) = -20 – 10 = -30.

D 2 = = 5(28 – 48) – (16 – 56) = -100 + 40 = -60.

D 3 = = 5(32 – 42) + (16 – 56) = -50 – 40 = -90.

Note 1. If the system is homogeneous, i.e. b i = 0, then for D¹0 the system has a unique zero solution x 1 = x 2 = … = x n = 0.

Note 2. At D=0 the system has an infinite number of solutions.

Inverse matrix method.

The matrix method is applicable to solving systems of equations where the number of equations is equal to the number of unknowns.

Let the system of equations be given: Let's create matrices:

A= - matrix of coefficients for variables or matrix of the system;

B = - matrix – column of free terms;

X = - matrix – column of unknowns.

Then the system of equations can be written: A×X = B. Let us multiply both sides of the equality from the left by A -1: A -1 ×A×X = A -1 ×B, because A -1 ×A = E, That E×X = A -1 ×B, then the following formula is valid:

X = A -1 ×B

Thus, to apply this method it is necessary to find inverse matrix.

Example. Solve the system of equations:

X = , B = , A =

Let's find the inverse matrix A -1.

D = det A = 5(4-9) + 1(2 – 12) – 1(3 – 8) = -25 – 10 +5 = -30≠0 ⇒ the inverse matrix exists.

M 11 = ; M 21 = ; M 31 = ;

M 12 = M 22 = M 32 =

M 13 = M 23 = M 33 =

A -1 = ;

Let's check:

A×A -1 =
=E.

Finding the X matrix.

X = = A -1 B = × = .

We received the system solutions: x =1; y = 2; z = 3.

4.Gauss method.

Let the system be given m linear equations with n unknown:

Assuming that the coefficient in the system a 11 is different from zero (if this is not the case, then the equation with a nonzero coefficient at x 1). We transform the system as follows: leave the first equation unchanged, and exclude the unknown from all other equations x 1 using equivalent transformations in the manner described above.

In the resulting system

,

assuming that (which can always be obtained by rearranging equations or terms within equations), we leave the first two equations of the system unchanged, and from the remaining equations, using the second equation, we eliminate the unknown with the help of elementary transformations x 2. In the newly received system

provided we leave the first three equations unchanged, and of all the rest, use the third equation elementary transformations exclude the unknown x 3 .

This process continues until one of three possible cases occurs:

1) if as a result we arrive at a system, one of the equations of which has zero coefficients for all unknowns and a nonzero free term, then the original system is inconsistent;

2) if as a result of transformations we obtain a system with a triangular matrix of coefficients, then the system is consistent and definite;

3) if a stepwise system of coefficients is obtained (and the condition of point 1 is not met), then the system is consistent and indefinite.

Consider the square system : (1)

This system has a coefficient a 11 is different from zero. If this condition were not met, then in order to obtain it, it would be necessary to rearrange the equations, putting first the equation whose coefficient at x 1 is not equal to zero.

We will carry out the following system transformations:

1) because a 11 ¹0, we leave the first equation unchanged;

2) instead of the second equation, we write the equation obtained if we subtract the first multiplied by 4 from the second equation;

3) instead of the third equation, we write the difference between the third and the first, multiplied by 3;

4) instead of the fourth equation, we write the difference between the fourth and the first, multiplied by 5.

The resulting new system is equivalent to the original one and has zero coefficients in all equations except the first one. x 1 (this was the purpose of transformations 1 – 4): (2)

For the above transformation and for all further transformations, you should not completely rewrite the entire system, as was just done. The original system can be represented as a matrix

. (3)

Matrix (3) is called extended matrix for the original system of equations. If we remove the column of free terms from the extended matrix, we get system coefficient matrix, which is sometimes simply called matrix of the system.

System (2) corresponds to the extended matrix

.

Let's transform this matrix as follows:

1) we will leave the first two lines unchanged, since the element a 22 is not zero;

2) instead of the third line, we write the difference between the second line and double the third;

3) replace the fourth line with the difference between the second line doubled and the fourth line multiplied by 5.

The result is a matrix corresponding to a system whose unknown x 1 is excluded from all equations except the first, and the unknown x 2 - from all equations except the first and second:

.

Now let's exclude the unknown x 3 from the fourth equation. To do this, we transform the last matrix as follows:

1) we will leave the first three lines unchanged, since a 33¹0;

2) replace the fourth line with the difference between the third, multiplied by 39, and the fourth: .

The resulting matrix corresponds to the system

. (4)

From the last equation of this system we obtain x 4 = 2. Substituting this value into the third equation, we get x 3 = 3. Now from the second equation it follows that x 2 = 1, and from the first - x 1 = –1. It is obvious that the resulting solution is unique (since the value is determined in the only way x 4 then x 3, etc.).

Definition: Let's call a square matrix that has non-zero numbers on the main diagonal and zeros below the main diagonal, triangular matrix.

The coefficient matrix of system (4) is a triangular matrix.

Comment: If, using elementary transformations, the coefficient matrix square system can be reduced to a triangular matrix, then the system is consistent and definite.

Let's look at another example: . (5)

Let us carry out the following transformations of the extended matrix of the system:

1) leave the first line unchanged;

2) instead of the second line, write the difference between the second line and double the first;

3) instead of the third line, we write the difference between the third line and triple the first;

4) replace the fourth line with the difference between the fourth and first;

5) replace the fifth line with the difference of the fifth line and double the first.

As a result of transformations, we obtain the matrix

.

Leaving the first two rows of this matrix unchanged, we reduce it to the following form by elementary transformations:

.

If now, following the Gauss method, which is also called the method of sequential elimination of unknowns, using the third line we bring the coefficients at x 3 in the fourth and fifth rows, then after dividing all elements of the second row by 5 and dividing all elements of the third row by 2, we obtain the matrix

.

Each of the last two rows of this matrix corresponds to the equation 0 x 1 +0x 2 +0x 3 +0x 4 +0x 5 = 0. This equation is satisfied by any set of numbers x 1 ,x 2, ¼, x 5 and should be removed from the system. Thus, the system with the just obtained extended matrix is ​​equivalent to a system with an extended matrix of the form

. (6)

The last row of this matrix corresponds to the equation
x 3 – 2x 4 + 3x 5 = –4. If unknown x 4 and x 5 give arbitrary values: x 4 = C 1; x 5 = C 2, then from the last equation of the system corresponding to matrix (6), we obtain x 3 = –4 + 2C 1 – 3C 2. Substituting expressions x 3 ,x 4, and x 5 into the second equation of the same system, we get x 2 = –3 + 2C 1 – 2C 2. Now from the first equation we can get x 1 = 4 – C 1+ C 2. The final solution of the system is presented in the form .

Consider a rectangular matrix A, whose number of columns m more than number of lines n. Such a matrix A let's call stepped.

It is obvious that matrix (6) is a step matrix.

If, when applying equivalent transformations to a system of equations, at least one equation is reduced to the form

0x 1 + 0x 2 + ¼0 x n = b j (b j ¹ 0),

then the system is incompatible or contradictory, since not a single set of numbers x 1 , x 2, ¼, x n does not satisfy this equation.

If, when transforming the extended matrix of the system, the matrix of coefficients is reduced to a stepwise form and the system does not turn out to be inconsistent, then the system is consistent and indefinite, that is, it has infinitely many solutions.

In the latter system, all solutions can be obtained by assigning specific numerical values ​​to the parameters C 1 And C 2.

Definition: Those variables whose coefficients are on the main diagonal of the step matrix (this means that these coefficients are different from zero) are called o main. In the example discussed above, these are the unknowns x 1 , x 2 , x 3. The remaining variables are called non-core. In the example above, these are the variables x 4, and x 5 . Non-primary variables can be given any values ​​or expressed through parameters, as was done in the last example.

Core variables are uniquely expressed through noncore variables.

Definition: If non-main variables are given specific numerical values ​​and the main variables are expressed through them, then the resulting solution is called private solution.

Definition: If non-basic variables are expressed in terms of parameters, then a solution is obtained, which is called general solution.

Definition: If all non-basic variables are given zero values, then the resulting solution is called basic.

Comment: The same system can sometimes be reduced to different sets of basic variables. So, for example, you can swap the 3rd and 4th columns in matrix (6). Then the main variables will be x 1 , x 2 ,x 4, and non-main ones - x 3 and x 5 .

Definition: If two different sets of basic variables are obtained at in various ways finding a solution to the same system, then these sets necessarily contain the same number of variables, called system rank.

Let's consider another system that has infinitely many solutions: .

Let us transform the extended matrix of the system using the Gaussian method:

.

As you can see, we did not get a step matrix, but the last matrix can be transformed by swapping the third and fourth columns: .

This matrix is ​​already stepped. The corresponding system has two non-basic variables - x 3 , x 5 and three main ones - x 1 , x 2 , x 4 . The solution to the original system is presented in the following form:

Here is an example of a system that has no solution:

.

Let's transform the system matrix using the Gaussian method:

.

The last row of the last matrix corresponds to the unsolvable equation 0x 1 + 0x 2 + 0x 3 = 1. Consequently, the original system is inconsistent.

Lecture No. 3.

Topic: Vectors. Scalar, vector and mixed product of vectors

1. The concept of a vector. Collinearity, orthogonality and coplanarity of vectors.

2. Linear operation on vectors.

3. Scalar product vectors and its application

4. Cross product of vectors and its application

5. Mixed product of vectors and its application

1. The concept of a vector. Collinarity, orthogonality and coplanarity of vectors.

Definition: A vector is a directed segment with a starting point A and an ending point B.

Designation: , ,

Definition: The length or modulus of a vector vector is a number equal to the length of the segment AB representing the vector.

Definition: A vector is called zero if the beginning and end of the vector coincide.

Definition: A vector of unit length is called unit. Definition: Vectors are called collinear if they lie on the same line or on parallel lines ( || ).

Comment:

1.Collinear vectors can be directed identically or oppositely.

2. The zero vector is considered collinear to any vector.

Definition: Two vectors are said to be equal if they are collinear,

have the same directions and have the same lengths ( = )

Systems of equations have been widely used in the economic industry with mathematical modeling various processes. For example, when solving problems of production management and planning, logistics routes ( transport problem) or equipment placement.

Systems of equations are used not only in mathematics, but also in physics, chemistry and biology, when solving problems of finding population size.

A system of linear equations is two or more equations with several variables for which it is necessary to find a common solution. Such a sequence of numbers for which all equations become true equalities or prove that the sequence does not exist.

Linear equation

Equations of the form ax+by=c are called linear. The designations x, y are the unknowns whose value must be found, b, a are the coefficients of the variables, c is the free term of the equation.
Solving an equation by plotting it will look like a straight line, all points of which are solutions to the polynomial.

Types of systems of linear equations

The simplest examples are considered to be systems of linear equations with two variables X and Y.

F1(x, y) = 0 and F2(x, y) = 0, where F1,2 are functions and (x, y) are function variables.

Solve system of equations - this means finding values ​​(x, y) at which the system turns into a true equality or establishing that suitable values ​​of x and y do not exist.

A pair of values ​​(x, y), written as the coordinates of a point, is called a solution to a system of linear equations.

If systems have one common solution or no solution exists, they are called equivalent.

Homogeneous systems of linear equations are systems whose right-hand side is equal to zero. If the right part after the equal sign has a value or is expressed by a function, such a system is heterogeneous.

The number of variables can be much more than two, then we should talk about an example of a system of linear equations with three or more variables.

When faced with systems, schoolchildren assume that the number of equations must necessarily coincide with the number of unknowns, but this is not the case. The number of equations in the system does not depend on the variables; there can be as many of them as desired.

Simple and complex methods for solving systems of equations

There is no general analytical method for solving such systems; all methods are based on numerical solutions. The school mathematics course describes in detail such methods as permutation, algebraic addition, substitution, as well as graphical and matrix method, solution by Gaussian method.

The main task when teaching solution methods is to teach how to correctly analyze the system and find the optimal solution algorithm for each example. The main thing is not to memorize a system of rules and actions for each method, but to understand the principles of using a particular method

Solving examples of systems of linear equations of the 7th grade program secondary school quite simple and explained in great detail. In any mathematics textbook, this section is given enough attention. Solving examples of systems of linear equations using the Gauss and Cramer method is studied in more detail in the first years of higher education.

Solving systems using the substitution method

The actions of the substitution method are aimed at expressing the value of one variable in terms of the second. The expression is substituted into the remaining equation, then it is reduced to a form with one variable. The action is repeated depending on the number of unknowns in the system

Let us give a solution to an example of a system of linear equations of class 7 using the substitution method:

As can be seen from the example, the variable x was expressed through F(X) = 7 + Y. The resulting expression, substituted into the 2nd equation of the system in place of X, helped to obtain one variable Y in the 2nd equation. Solving this example is easy and allows you to get the Y value. The last step is to check the obtained values.

It is not always possible to solve an example of a system of linear equations by substitution. The equations can be complex and expressing the variable in terms of the second unknown will be too cumbersome for further calculations. When there are more than 3 unknowns in the system, solving by substitution is also inappropriate.

Solution of an example of a system of linear inhomogeneous equations:

Solution using algebraic addition

When searching for solutions to systems using the addition method, equations are added term by term and multiplied by various numbers. The ultimate goal of mathematical operations is an equation in one variable.

Application of this method requires practice and observation. Solving a system of linear equations using the addition method when there are 3 or more variables is not easy. Algebraic addition is convenient to use when equations contain fractions and decimals.

Solution algorithm:

1. Multiply both sides of the equation by a certain number. As a result arithmetic action one of the coefficients of the variable must become equal to 1.
2. Add the resulting expression term by term and find one of the unknowns.
3. Substitute the resulting value into the 2nd equation of the system to find the remaining variable.

Method of solution by introducing a new variable

A new variable can be introduced if the system requires finding a solution for no more than two equations; the number of unknowns should also be no more than two.

The method is used to simplify one of the equations by introducing a new variable. The new equation is solved for the introduced unknown, and the resulting value is used to determine the original variable.

The example shows that by introducing a new variable t, it was possible to reduce the 1st equation of the system to a standard quadratic trinomial. You can solve a polynomial by finding the discriminant.

It is necessary to find the value of the discriminant using the well-known formula: D = b2 - 4*a*c, where D is the desired discriminant, b, a, c are the factors of the polynomial. IN given example a=1, b=16, c=39, therefore D=100. If the discriminant is greater than zero, then there are two solutions: t = -b±√D / 2*a, if the discriminant is less than zero, then there is one solution: x = -b / 2*a.

The solution for the resulting systems is found by addition.

Visual method for solving systems

Suitable for 3 equation systems. The method consists in constructing graphs of each equation included in the system on the coordinate axis. The coordinates of the intersection points of the curves will be the general solution of the system.

The graphical method has a number of nuances. Let's look at several examples of solving systems of linear equations in a visual way.

As can be seen from the example, for each line two points were constructed, the values ​​of the variable x were chosen arbitrarily: 0 and 3. Based on the values ​​of x, the values ​​for y were found: 3 and 0. Points with coordinates (0, 3) and (3, 0) were marked on the graph and connected by a line.

The steps must be repeated for the second equation. The point of intersection of the lines is the solution of the system.

The following example requires finding a graphical solution to a system of linear equations: 0.5x-y+2=0 and 0.5x-y-1=0.

As can be seen from the example, the system has no solution, because the graphs are parallel and do not intersect along their entire length.

The systems from examples 2 and 3 are similar, but when constructed it becomes obvious that their solutions are different. It should be remembered that it is not always possible to say whether a system has a solution or not; it is always necessary to construct a graph.

The matrix and its varieties

Matrices are used to concisely write a system of linear equations. A matrix is ​​a special type of table filled with numbers. n*m has n - rows and m - columns.

A matrix is ​​square when the number of columns and rows are equal. A matrix-vector is a matrix of one column with an infinitely possible number of rows. A matrix with ones along one of the diagonals and other zero elements is called identity.

An inverse matrix is ​​a matrix when multiplied by which the original one turns into a unit matrix; such a matrix exists only for the original square one.

Rules for converting a system of equations into a matrix

In relation to systems of equations, the coefficients and free terms of the equations are written as matrix numbers; one equation is one row of the matrix.

A matrix row is said to be nonzero if at least one element of the row is not zero. Therefore, if in any of the equations the number of variables differs, then it is necessary to enter zero in place of the missing unknown.

The matrix columns must strictly correspond to the variables. This means that the coefficients of the variable x can be written only in one column, for example the first, the coefficient of the unknown y - only in the second.

When multiplying a matrix, all elements of the matrix are sequentially multiplied by a number.

Options for finding the inverse matrix

The formula for finding the inverse matrix is ​​quite simple: K -1 = 1 / |K|, where K -1 is the inverse matrix, and |K| is the determinant of the matrix. |K| must not be equal to zero, then the system has a solution.

The determinant is easily calculated for a two-by-two matrix; you just need to multiply the diagonal elements by each other. For the “three by three” option, there is a formula |K|=a 1 b 2 c 3 + a 1 b 3 c 2 + a 3 b 1 c 2 + a 2 b 3 c 1 + a 2 b 1 c 3 + a 3 b 2 c 1 . You can use the formula, or you can remember that you need to take one element from each row and each column so that the numbers of columns and rows of elements are not repeated in the work.

Solving examples of systems of linear equations using the matrix method

The matrix method of finding a solution allows you to reduce cumbersome entries when solving systems with big amount variables and equations.

In the example, a nm are the coefficients of the equations, the matrix is ​​a vector x n are variables, and b n are free terms.

Solving systems using the Gaussian method

IN higher mathematics The Gaussian method is studied together with the Cramer method, and the process of finding solutions to systems is called the Gauss-Cramer solution method. These methods are used to find variables of systems with a large number of linear equations.

The Gauss method is very similar to solutions by substitution and algebraic addition, but is more systematic. In the school course, the solution by the Gaussian method is used for systems of 3 and 4 equations. The purpose of the method is to reduce the system to the form of an inverted trapezoid. By means of algebraic transformations and substitutions, the value of one variable is found in one of the equations of the system. The second equation is an expression with 2 unknowns, while 3 and 4 are, respectively, with 3 and 4 variables.

After bringing the system to the described form, the further solution is reduced to the sequential substitution of known variables into the equations of the system.

In school textbooks for grade 7, an example of a solution by the Gauss method is described as follows:

As can be seen from the example, at step (3) two equations were obtained: 3x 3 -2x 4 =11 and 3x 3 +2x 4 =7. Solving any of the equations will allow you to find out one of the variables x n.

Theorem 5, which is mentioned in the text, states that if one of the equations of the system is replaced by an equivalent one, then the resulting system will also be equivalent to the original one.

The Gauss method is difficult for students to understand high school, but is one of the most interesting ways to develop the ingenuity of children enrolled in advanced learning programs in math and physics classes.

For ease of recording, calculations are usually done as follows:

The coefficients of the equations and free terms are written in the form of a matrix, where each row of the matrix corresponds to one of the equations of the system. separates the left side of the equation from the right. Roman numerals indicate the numbers of equations in the system.

First, write down the matrix to be worked with, then all the actions carried out with one of the rows. The resulting matrix is ​​written after the "arrow" sign and continues to perform the necessary algebraic operations until the result is achieved.

The result should be a matrix in which one of the diagonals is equal to 1, and all other coefficients are equal to zero, that is, the matrix is ​​reduced to a unit form. We must not forget to perform calculations with numbers on both sides of the equation.

This recording method is less cumbersome and allows you not to be distracted by listing numerous unknowns.

The free use of any solution method will require care and some experience. Not all methods are of an applied nature. Some methods of finding solutions are more preferable in a particular area of ​​human activity, while others exist for educational purposes.

A system of m linear equations with n unknowns called a system of the form

Where a ij And b i (i=1,…,m; b=1,…,n) are some known numbers, and x 1 ,…,x n– unknown. In the designation of coefficients a ij first index i denotes the equation number, and the second j– the number of the unknown at which this coefficient stands.

We will write the coefficients for the unknowns in the form of a matrix , which we'll call matrix of the system.

The numbers on the right side of the equations are b 1 ,…,b m are called free members.

Totality n numbers c 1 ,…,c n called decision of a given system, if each equation of the system becomes an equality after substituting numbers into it c 1 ,…,c n instead of the corresponding unknowns x 1 ,…,x n.

Our task will be to find solutions to the system. In this case, three situations may arise:

A system of linear equations that has at least one solution is called joint. Otherwise, i.e. if the system has no solutions, then it is called non-joint.

Let's consider ways to find solutions to the system.

MATRIX METHOD FOR SOLVING SYSTEMS OF LINEAR EQUATIONS

Matrices make it possible to briefly write down a system of linear equations. Let a system of 3 equations with three unknowns be given:

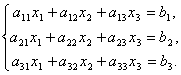
Consider the system matrix and matrices columns of unknown and free terms

Let's find the work

those. as a result of the product, we obtain the left-hand sides of the equations of this system. Then, using the definition of matrix equality, this system can be written in the form

or shorter A∙X=B.

Here are the matrices A And B are known, and the matrix X unknown. It is necessary to find it, because... its elements are the solution to this system. This equation is called matrix equation.

Let the matrix determinant be different from zero | A| ≠ 0. Then the matrix equation is solved as follows. Multiply both sides of the equation on the left by the matrix A-1, inverse of the matrix A: . Because the A -1 A = E And E∙X = X, then we obtain a solution to the matrix equation in the form X = A -1 B .

Note that since the inverse matrix can only be found for square matrices, the matrix method can only solve those systems in which the number of equations coincides with the number of unknowns. However, matrix recording of the system is also possible in the case when the number of equations is not equal to the number of unknowns, then the matrix A will not be square and therefore it is impossible to find a solution to the system in the form X = A -1 B.

Examples. Solve systems of equations.

CRAMER'S RULE

Consider a system of 3 linear equations with three unknowns:

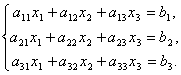
Third-order determinant corresponding to the system matrix, i.e. composed of coefficients for unknowns,

called determinant of the system.

Let's compose three more determinants as follows: replace sequentially 1, 2 and 3 columns in the determinant D with a column of free terms

Then we can prove the following result.

Theorem (Cramer's rule). If the determinant of the system Δ ≠ 0, then the system under consideration has one and only one solution, and

Proof. So, let's consider a system of 3 equations with three unknowns. Let's multiply the 1st equation of the system by the algebraic complement A 11 element a 11, 2nd equation – on A 21 and 3rd – on A 31:

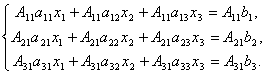
Let's add these equations:

Let's look at each of the brackets and the right side of this equation. By the theorem on the expansion of the determinant in elements of the 1st column

Similarly, it can be shown that and .

Finally, it is easy to notice that

Thus, we obtain the equality: .

Hence, .

The equalities and are derived similarly, from which the statement of the theorem follows.

Thus, we note that if the determinant of the system Δ ≠ 0, then the system has a unique solution and vice versa. If the determinant of the system is equal to zero, then the system either has an infinite number of solutions or has no solutions, i.e. incompatible.

Examples. Solve system of equations

GAUSS METHOD

The previously discussed methods can be used to solve only those systems in which the number of equations coincides with the number of unknowns, and the determinant of the system must be different from zero. The Gauss method is more universal and suitable for systems with any number of equations. It consists in the consistent elimination of unknowns from the equations of the system.

Consider again a system of three equations with three unknowns:

.

We will leave the first equation unchanged, and from the 2nd and 3rd we will exclude the terms containing x 1. To do this, divide the second equation by A 21 and multiply by – A 11, and then add it to the 1st equation. Similarly, we divide the third equation by A 31 and multiply by – A 11, and then add it with the first one. As a result, the original system will take the form:

Now from the last equation we eliminate the term containing x 2. To do this, divide the third equation by, multiply by and add with the second. Then we will have a system of equations:

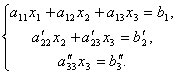
From here, from the last equation it is easy to find x 3, then from the 2nd equation x 2 and finally, from 1st - x 1.

When using the Gaussian method, the equations can be swapped if necessary.

Often instead of writing new system equations, are limited to writing out the extended matrix of the system:

and then bring it to a triangular or diagonal form using elementary transformations.

TO elementary transformations matrices include the following transformations:

1. rearranging rows or columns;
2. multiplying a string by a number other than zero;
3. adding other lines to one line.

Examples: Solve systems of equations using the Gauss method.

Thus, the system has an infinite number of solutions.