Cramer method solution diagram. Cramer's method for solving systems of linear equations

In the first part, we looked at some theoretical material, the substitution method, as well as the method of term-by-term addition of system equations. I recommend everyone who accessed the site through this page to read the first part. Perhaps some visitors will find the material too simple, but in the process of solving systems of linear equations, I made a number of very important comments and conclusions regarding the solution of mathematical problems in general.

And now we will analyze Cramer’s rule, as well as solving a system of linear equations using inverse matrix(matrix method). All materials are presented simply, in detail and clearly; almost all readers will be able to learn how to solve systems using the above methods.

First, we will take a closer look at Cramer's rule for a system of two linear equations in two unknowns. For what? – After all, the simplest system can be solved using the school method, the method of term-by-term addition!

The fact is that, albeit sometimes, such a task occurs - to solve a system of two linear equations with two unknowns using Cramer's formulas. Secondly, a simpler example will help you understand how to use Cramer's rule to more complex case– systems of three equations with three unknowns.

In addition, there are systems of linear equations with two variables, which are advisable to solve using Cramer’s rule!

Consider the system of equations

At the first step, we calculate the determinant, it is called main determinant of the system.

Gauss method.

If , then the system has only decision, and to find the roots we must calculate two more determinants:
And

In practice, the above qualifiers can also be denoted by a Latin letter.

We find the roots of the equation using the formulas:
,

Example 7

Solve a system of linear equations

Solution: We see that the coefficients of the equation are quite large, on the right side there are decimals with a comma. The comma is a rather rare guest in practical tasks in mathematics; I took this system from an econometric problem.

How to solve such a system? You can try to express one variable in terms of another, but in this case you will probably end up with terrible fancy fractions that are extremely inconvenient to work with, and the design of the solution will look simply terrible. You can multiply the second equation by 6 and subtract term by term, but the same fractions will arise here too.

What to do? In such cases, Cramer's formulas come to the rescue.

;

;

Answer: ,

Both roots have infinite tails and are found approximately, which is quite acceptable (and even commonplace) for econometrics problems.

No comments are needed here, since the task is solved according to ready-made formulas, however, there is one caveat. When using this method, compulsory A fragment of the task design is the following fragment: “This means that the system has a unique solution”. Otherwise, the reviewer may punish you for disrespect for Cramer's theorem.

It would not be superfluous to check, which can be conveniently carried out on a calculator: we substitute approximate values ​​into the left side of each equation of the system. As a result, with a small error, you should get numbers that are on the right sides.

Example 8

Present the answer in ordinary improper fractions. Do a check.

This is an example for independent decision(example of finishing and answer at the end of the lesson).

Let's move on to consider Cramer's rule for a system of three equations with three unknowns:

We find the main determinant of the system:

If , then the system has infinitely many solutions or is inconsistent (has no solutions). In this case, Cramer's rule will not help; you need to use the Gauss method.

If , then the system has a unique solution and to find the roots we must calculate three more determinants:
, ,

And finally, the answer is calculated using the formulas:

As you can see, the “three by three” case is fundamentally no different from the “two by two” case; the column of free terms sequentially “walks” from left to right along the columns of the main determinant.

Example 9

Solve the system using Cramer's formulas.

Solution: Let's solve the system using Cramer's formulas.

, which means the system has a unique solution.

Answer: .

Actually, here again there is nothing special to comment on, due to the fact that the solution follows ready-made formulas. But there are a couple of comments.

It happens that as a result of calculations, “bad” irreducible fractions are obtained, for example: .
I recommend the following “treatment” algorithm. If you don’t have a computer at hand, do this:

1) There may be an error in the calculations. As soon as you encounter a “bad” fraction, you immediately need to check Is the condition rewritten correctly?. If the condition is rewritten without errors, then you need to recalculate the determinants using expansion in another row (column).

2) If no errors are identified as a result of checking, then most likely there was a typo in the task conditions. In this case, calmly and CAREFULLY work through the task to the end, and then be sure to check and we draw it up on a clean sheet after the decision. Of course, checking a fractional answer is an unpleasant task, but it will be a disarming argument for the teacher, who really likes to give a minus for any bullshit like . How to handle fractions is described in detail in the answer to Example 8.

If you have a computer at hand, then use an automated program to check, which can be downloaded for free at the very beginning of the lesson. By the way, it is most profitable to use the program right away (even before starting the solution); you will immediately see the intermediate step where you made a mistake! The same calculator automatically calculates the solution to the system matrix method.

Second remark. From time to time there are systems in the equations of which some variables are missing, for example:

Here in the first equation there is no variable , in the second there is no variable . In such cases, it is very important to correctly and CAREFULLY write down the main determinant:
– zeros are placed in place of missing variables.
By the way, it is rational to open determinants with zeros according to the row (column) in which the zero is located, since there are noticeably fewer calculations.

Example 10

Solve the system using Cramer's formulas.

This is an example for an independent solution (a sample of the final design and the answer at the end of the lesson).

For the case of a system of 4 equations with 4 unknowns, Cramer’s formulas are written according to similar principles. You can see a live example in the lesson Properties of Determinants. Reducing the order of the determinant - five 4th order determinants are quite solvable. Although the task is already very reminiscent of a professor’s shoe on the chest of a lucky student.

Solving the system using an inverse matrix

The inverse matrix method is essentially special case matrix equation(See Example No. 3 of the specified lesson).

To study this section, you must be able to expand determinants, find the inverse of a matrix, and perform matrix multiplication. Relevant links will be provided as the explanations progress.

Example 11

Solve the system using the matrix method

Solution: Let's write the system in matrix form:
, Where

Please look at the system of equations and matrices. I think everyone understands the principle by which we write elements into matrices. The only comment: if some variables were missing from the equations, then zeros would have to be placed in the corresponding places in the matrix.

We find the inverse matrix using the formula:
, where is the transposed matrix of algebraic complements of the corresponding elements of the matrix.

First, let's look at the determinant:

Here the determinant is expanded on the first line.

Attention! If , then the inverse matrix does not exist, and it is impossible to solve the system using the matrix method. In this case, the system is solved by the method of eliminating unknowns (Gauss method).

Now we need to calculate 9 minors and write them into the minors matrix

Reference: It is useful to know the meaning of double subscripts in linear algebra. The first digit is the number of the line in which the element is located. The second digit is the number of the column in which the element is located:

That is, a double subscript indicates that the element is in the first row, third column, and, for example, the element is in 3 row, 2 column

Cramer's method is based on the use of determinants in solving systems of linear equations. This significantly speeds up the solution process.

Cramer's method can be used to solve a system of as many linear equations as there are unknowns in each equation. If the determinant of the system is not equal to zero, then Cramer’s method can be used in the solution, but if it is equal to zero, then it cannot. In addition, Cramer's method can be used to solve systems of linear equations that have a unique solution.

Definition. A determinant made up of coefficients for unknowns is called a determinant of the system and is denoted (delta).

Determinants

are obtained by replacing the coefficients of the corresponding unknowns with free terms:

;

.

Cramer's theorem. If the determinant of the system is nonzero, then the system of linear equations has one unique solution, and the unknown is equal to the ratio of the determinants. The denominator contains the determinant of the system, and the numerator contains the determinant obtained from the determinant of the system by replacing the coefficients of this unknown with free terms. This theorem holds for a system of linear equations of any order.

Example 1. Solve a system of linear equations:

According to Cramer's theorem we have:

So, the solution to system (2):

online calculator, decisive method Kramer.

Three cases when solving systems of linear equations

As is clear from Cramer's theorem, when solving a system of linear equations, three cases can occur:

First case: a system of linear equations has a unique solution

(the system is consistent and definite)

Second case: a system of linear equations has an infinite number of solutions

(the system is consistent and uncertain)

** ,

those. the coefficients of the unknowns and the free terms are proportional.

Third case: the system of linear equations has no solutions

(the system is inconsistent)

So the system m linear equations with n called variables non-joint, if she does not have a single solution, and joint, if it has at least one solution. Joint system equations that have only one solution is called certain, and more than one – uncertain.

Examples of solving systems of linear equations using the Cramer method

Let the system be given

.

Based on Cramer's theorem

………….
,

Where
-

system determinant. We obtain the remaining determinants by replacing the column with the coefficients of the corresponding variable (unknown) with free terms:

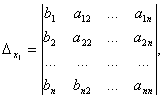
Example 2.

.

Therefore, the system is definite. To find its solution, we calculate the determinants

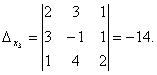
Using Cramer's formulas we find:

So, (1; 0; -1) is the only solution to the system.

To check solutions to systems of equations 3 X 3 and 4 X 4, you can use an online calculator using Cramer's solving method.

If in a system of linear equations there are no variables in one or more equations, then in the determinant the corresponding elements are equal to zero! This is the next example.

Example 3. Solve a system of linear equations using the Cramer method:

.

Solution. We find the determinant of the system:

Look carefully at the system of equations and at the determinant of the system and repeat the answer to the question in which cases one or more elements of the determinant are equal to zero. So, the determinant is not equal to zero, therefore the system is definite. To find its solution, we calculate the determinants for the unknowns

Using Cramer's formulas we find:

So, the solution to the system is (2; -1; 1).

To check solutions to systems of equations 3 X 3 and 4 X 4, you can use an online calculator using Cramer's solving method.

Top of page

We continue to solve systems using Cramer's method together

As already mentioned, if the determinant of the system is equal to zero, and the determinants of the unknowns are not equal to zero, the system is inconsistent, that is, it has no solutions. Let us illustrate with the following example.

Example 6. Solve a system of linear equations using the Cramer method:

Solution. We find the determinant of the system:

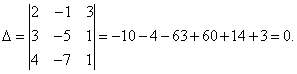
The determinant of the system is equal to zero, therefore, the system of linear equations is either inconsistent and definite, or inconsistent, that is, has no solutions. To clarify, we calculate determinants for unknowns

The determinants of the unknowns are not equal to zero, therefore, the system is inconsistent, that is, it has no solutions.

To check solutions to systems of equations 3 X 3 and 4 X 4, you can use an online calculator using Cramer's solving method.

In problems involving systems of linear equations, there are also those where, in addition to letters denoting variables, there are also other letters. These letters represent a number, most often real. In practice, such equations and systems of equations are led to by problems of searching for general properties of any phenomena or objects. That is, have you invented any new material or a device, and to describe its properties, which are common regardless of the size or number of an instance, you need to solve a system of linear equations, where instead of some coefficients for variables there are letters. You don't have to look far for examples.

The following example is for a similar problem, only the number of equations, variables, and letters denoting a certain real number increases.

Example 8. Solve a system of linear equations using the Cramer method:

Solution. We find the determinant of the system:

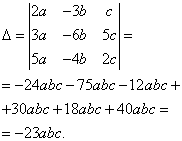
Finding determinants for unknowns

Methods Kramer And Gauss- one of the most popular solution methods SLAU. In addition, in some cases it is advisable to use specific methods. The session is close, and now is the time to repeat or master them from scratch. Today we’ll look at the solution using Cramer’s method. After all, solving a system of linear equations using the Cramer method is a very useful skill.

Systems of linear algebraic equations

Linear system algebraic equations– system of equations of the form:

Value set x , in which the equations of the system turn into identities, is called a solution of the system, a And b are real coefficients. A simple system consisting of two equations with two unknowns can be solved in your head or by expressing one variable in terms of the other. But there can be much more than two variables (xes) in a SLAE, and here simple school manipulations are not enough. What to do? For example, solve SLAEs using Cramer's method!

So, let the system consist of n equations with n unknown.

Such a system can be rewritten in matrix form

Here A – the main matrix of the system, X And B , respectively, column matrices of unknown variables and free terms.

Solving SLAEs using Cramer's method

If the determinant of the main matrix is ​​not equal to zero (the matrix is ​​non-singular), the system can be solved using Cramer's method.

According to Cramer's method, the solution is found using the formulas:

Here delta is the determinant of the main matrix, and delta x nth – determinant obtained from the determinant of the main matrix by replacing the nth column with a column of free terms.

This is the whole essence of the Cramer method. Substituting the values ​​found using the above formulas x into the desired system, we are convinced of the correctness (or vice versa) of our solution. To help you quickly grasp the essence, we give below an example of a detailed solution of SLAE using Cramer’s method:

Even if you don't succeed the first time, don't be discouraged! With a little practice, you will start cracking SLAUs like nuts. Moreover, now it is absolutely not necessary to pore over a notebook, solving cumbersome calculations and filling up the core. You can easily solve SLAEs using Cramer’s method online, just by substituting ready-made form coefficients. Try it online calculator Solutions using Cramer's method can be found, for example, on this website.

And if the system turns out to be stubborn and does not give up, you can always turn to our authors for help, for example, to. If there are at least 100 unknowns in the system, we will definitely solve it correctly and on time!

With the same number of equations as the number of unknowns with the main determinant of the matrix, which is not equal to zero, the coefficients of the system (for such equations there is a solution and there is only one).

Cramer's theorem.

When the determinant of a matrix square system non-zero, which means that the system is consistent and it has one solution and it can be found by Cramer's formulas:

where Δ - determinant of the system matrix,

Δ i is the determinant of the system matrix, in which instead of i The th column contains the column of right sides.

When the determinant of a system is zero, it means that the system can become cooperative or incompatible.

This method is usually used for small systems with extensive calculations and if it is necessary to determine one of the unknowns. The complexity of the method is that many determinants need to be calculated.

Description of the Cramer method.

There is a system of equations:

A system of 3 equations can be solved using the Cramer method, which was discussed above for a system of 2 equations.

We compose a determinant from the coefficients of the unknowns:

It will be system determinant. When D≠0, which means the system is consistent. Now let's create 3 additional determinants:

,,

We solve the system by Cramer's formulas:

Examples of solving systems of equations using Cramer's method.

Example 1.

Given system:

Let's solve it using Cramer's method.

First you need to calculate the determinant of the system matrix:

Because Δ≠0, which means that from Cramer’s theorem the system is consistent and it has one solution. We calculate additional determinants. The determinant Δ 1 is obtained from the determinant Δ by replacing its first column with a column of free coefficients. We get:

In the same way, we obtain the determinant of Δ 2 from the determinant of the system matrix by replacing the second column with a column of free coefficients: