Solution using the inverse matrix method. Linear equations

System m linear equations with n unknowns called a system of the form

Where a ij And b i (i=1,…,m; b=1,…,n) are some known numbers, and x 1 ,…,x n– unknown. In the designation of coefficients a ij first index i denotes the equation number, and the second j– the number of the unknown at which this coefficient stands.

We will write the coefficients for the unknowns in the form of a matrix , which we'll call matrix of the system.

The numbers on the right side of the equations are b 1 ,…,b m are called free members.

Totality n numbers c 1 ,…,c n called decision of a given system, if each equation of the system becomes an equality after substituting numbers into it c 1 ,…,c n instead of the corresponding unknowns x 1 ,…,x n.

Our task will be to find solutions to the system. In this case, three situations may arise:

A system of linear equations that has at least one solution is called joint. Otherwise, i.e. if the system has no solutions, then it is called non-joint.

Let's consider ways to find solutions to the system.

MATRIX METHOD FOR SOLVING SYSTEMS OF LINEAR EQUATIONS

Matrices make it possible to briefly write down a system of linear equations. Let a system of 3 equations with three unknowns be given:

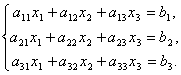
Consider the system matrix and matrices columns of unknown and free terms

Let's find the work

those. as a result of the product, we obtain the left-hand sides of the equations of this system. Then using the definition of matrix equality this system can be written in the form

or shorter A∙X=B.

Here are the matrices A And B are known, and the matrix X unknown. It is necessary to find it, because... its elements are the solution to this system. This equation is called matrix equation.

Let the determinant of the matrix be different from zero | A| ≠ 0. Then the matrix equation is solved as follows. Multiply both sides of the equation on the left by the matrix A-1, inverse of the matrix A: . Because the A -1 A = E And E∙X = X, then we get the solution matrix equation as X = A -1 B .

Note that since the inverse matrix can only be found for square matrices, then matrix method it is possible to solve only those systems in which the number of equations coincides with the number of unknowns. However, matrix recording of the system is also possible in the case when the number of equations is not equal to the number of unknowns, then the matrix A will not be square and therefore it is impossible to find a solution to the system in the form X = A -1 B.

Examples. Solve systems of equations.

CRAMER'S RULE

Consider a system of 3 linear equations with three unknowns:

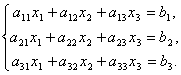
Third-order determinant corresponding to the system matrix, i.e. composed of coefficients for unknowns,

called determinant of the system.

Let's compose three more determinants as follows: replace sequentially 1, 2 and 3 columns in the determinant D with a column of free terms

Then we can prove the following result.

Theorem (Cramer's rule). If the determinant of the system Δ ≠ 0, then the system under consideration has one and only one solution, and

Proof. So, let's consider a system of 3 equations with three unknowns. Let's multiply the 1st equation of the system by the algebraic complement A 11 element a 11, 2nd equation – on A 21 and 3rd – on A 31:

Let's add these equations:

Let's look at each of the brackets and the right side of this equation. By the theorem on the expansion of the determinant in elements of the 1st column

Similarly, it can be shown that and .

Finally, it is easy to notice that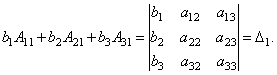

Thus, we obtain the equality: .

Hence, .

The equalities and are derived similarly, from which the statement of the theorem follows.

Thus, we note that if the determinant of the system Δ ≠ 0, then the system has only decision and back. If the determinant of the system is equal to zero, then the system either has an infinite number of solutions or has no solutions, i.e. incompatible.

Examples. Solve system of equations

GAUSS METHOD

The previously discussed methods can be used to solve only those systems in which the number of equations coincides with the number of unknowns, and the determinant of the system must be different from zero. The Gauss method is more universal and suitable for systems with any number of equations. It consists in the consistent elimination of unknowns from the equations of the system.

Consider again a system of three equations with three unknowns:

.

We will leave the first equation unchanged, and from the 2nd and 3rd we will exclude the terms containing x 1. To do this, divide the second equation by A 21 and multiply by – A 11, and then add it to the 1st equation. Similarly, we divide the third equation by A 31 and multiply by – A 11, and then add it with the first one. As a result, the original system will take the form:

Now from the last equation we eliminate the term containing x 2. To do this, divide the third equation by, multiply by and add with the second. Then we will have a system of equations:

From here, from the last equation it is easy to find x 3, then from the 2nd equation x 2 and finally, from 1st - x 1.

When using the Gaussian method, the equations can be swapped if necessary.

Often instead of writing new system equations, are limited to writing out the extended matrix of the system:

and then bring it to a triangular or diagonal form using elementary transformations.

TO elementary transformations matrices include the following transformations:

1. rearranging rows or columns;
2. multiplying a string by a number other than zero;
3. adding other lines to one line.

Examples: Solve systems of equations using the Gauss method.

Thus, the system has an infinite number of solutions.

In the first part, we looked at some theoretical material, the substitution method, as well as the method of term-by-term addition of system equations. I recommend everyone who accessed the site through this page to read the first part. Perhaps some visitors will find the material too simple, but in the process of solving systems of linear equations, I made a number of very important comments and conclusions regarding the solution of mathematical problems in general.

Now we will analyze Cramer’s rule, as well as solving a system of linear equations using an inverse matrix (matrix method). All materials are presented simply, in detail and clearly; almost all readers will be able to learn how to solve systems using the above methods.

First, we will take a closer look at Cramer's rule for a system of two linear equations in two unknowns. For what? – After all, the simplest system can be solved using the school method, the method of term-by-term addition!

The fact is that, albeit sometimes, such a task occurs - to solve a system of two linear equations with two unknowns using Cramer's formulas. Secondly, a simpler example will help you understand how to use Cramer's rule to more complex case– systems of three equations with three unknowns.

In addition, there are systems of linear equations with two variables, which are advisable to solve using Cramer’s rule!

Consider the system of equations

At the first step, we calculate the determinant, it is called main determinant of the system.

Gauss method.

If , then the system has a unique solution, and to find the roots we must calculate two more determinants:
And

In practice, the above qualifiers can also be denoted by a Latin letter.

We find the roots of the equation using the formulas:
,

Example 7

Solve a system of linear equations

Solution: We see that the coefficients of the equation are quite large, on the right side there are decimals with a comma. Comma - enough rare guest in practical tasks in mathematics, I took this system from an econometric problem.

How to solve such a system? You can try to express one variable in terms of another, but in this case you will probably end up with terrible fancy fractions that are extremely inconvenient to work with, and the design of the solution will look simply terrible. You can multiply the second equation by 6 and subtract term by term, but the same fractions will arise here too.

What to do? In such cases, Cramer's formulas come to the rescue.

;

;

Answer: ,

Both roots have infinite tails and are found approximately, which is quite acceptable (and even commonplace) for econometrics problems.

No comments are needed here, since the task is solved according to ready-made formulas However, there is one caveat. When using this method, compulsory A fragment of the task design is the following fragment: “This means that the system has a unique solution”. Otherwise, the reviewer may punish you for disrespect for Cramer's theorem.

It would not be superfluous to check, which can be conveniently carried out on a calculator: we substitute approximate values ​​into the left side of each equation of the system. As a result, with a small error, you should get numbers that are on the right sides.

Example 8

Present the answer in ordinary improper fractions. Do a check.

This is an example for independent decision(example of finishing and answer at the end of the lesson).

Let's move on to consider Cramer's rule for a system of three equations with three unknowns:

We find the main determinant of the system:

If , then the system has infinitely many solutions or is inconsistent (has no solutions). In this case, Cramer's rule will not help; you need to use the Gauss method.

If , then the system has a unique solution and to find the roots we must calculate three more determinants:
, ,

And finally, the answer is calculated using the formulas:

As you can see, the “three by three” case is fundamentally no different from the “two by two” case; the column of free terms sequentially “walks” from left to right along the columns of the main determinant.

Example 9

Solve the system using Cramer's formulas.

Solution: Let's solve the system using Cramer's formulas.

, which means the system has a unique solution.

Answer: .

Actually, here again there is nothing special to comment on, due to the fact that the solution follows ready-made formulas. But there are a couple of comments.

It happens that as a result of calculations, “bad” irreducible fractions are obtained, for example: .
I recommend the following “treatment” algorithm. If you don’t have a computer at hand, do this:

1) There may be an error in the calculations. As soon as you encounter a “bad” fraction, you immediately need to check Is the condition rewritten correctly?. If the condition is rewritten without errors, then you need to recalculate the determinants using expansion in another row (column).

2) If no errors are identified as a result of checking, then most likely there was a typo in the task conditions. In this case, calmly and CAREFULLY work through the task to the end, and then be sure to check and we draw it up on a clean sheet after the decision. Of course, checking a fractional answer is an unpleasant task, but it will be a disarming argument for the teacher, who really likes to give a minus for any bullshit like . How to handle fractions is described in detail in the answer to Example 8.

If you have a computer at hand, then use an automated program to check, which can be downloaded for free at the very beginning of the lesson. By the way, it is most profitable to use the program right away (even before starting the solution); you will immediately see the intermediate step where you made a mistake! The same calculator automatically calculates the solution of the system using the matrix method.

Second remark. From time to time there are systems in the equations of which some variables are missing, for example:

Here in the first equation there is no variable , in the second there is no variable . In such cases, it is very important to correctly and CAREFULLY write down the main determinant:
– zeros are placed in place of missing variables.
By the way, it is rational to open determinants with zeros according to the row (column) in which the zero is located, since there are noticeably fewer calculations.

Example 10

Solve the system using Cramer's formulas.

This is an example for an independent solution (a sample of the final design and the answer at the end of the lesson).

For the case of a system of 4 equations with 4 unknowns, Cramer’s formulas are written according to similar principles. You can see a live example in the lesson Properties of Determinants. Reducing the order of the determinant - five 4th order determinants are quite solvable. Although the task is already very reminiscent of a professor’s shoe on the chest of a lucky student.

Solving the system using an inverse matrix

The inverse matrix method is essentially special case matrix equation(See Example No. 3 of the specified lesson).

To study this section, you must be able to expand determinants, find the inverse of a matrix, and perform matrix multiplication. Relevant links will be provided as the explanations progress.

Example 11

Solve the system using the matrix method

Solution: Let's write the system in matrix form:
, Where

Please look at the system of equations and matrices. I think everyone understands the principle by which we write elements into matrices. The only comment: if some variables were missing from the equations, then zeros would have to be placed in the corresponding places in the matrix.

We find the inverse matrix using the formula:
, where is the transposed matrix of algebraic complements of the corresponding elements of the matrix.

First, let's look at the determinant:

Here the determinant is expanded on the first line.

Attention! If , then the inverse matrix does not exist, and it is impossible to solve the system using the matrix method. In this case, the system is solved by the method of eliminating unknowns (Gauss method).

Now we need to calculate 9 minors and write them into the minors matrix

Reference: It is useful to know the meaning of double subscripts in linear algebra. The first digit is the number of the line in which the element is located. The second digit is the number of the column in which the element is located:

That is, a double subscript indicates that the element is in the first row, third column, and, for example, the element is in 3 row, 2 column

This is a concept that summarizes everything possible operations, produced with matrices. Mathematical matrix - table of elements. About a table where m lines and n columns, this matrix is ​​said to have the dimension m on n.

General view of the matrix:

For matrix solutions It is necessary to understand what a matrix is ​​and know its main parameters. Main elements of the matrix:

• The main diagonal, consisting of elements a 11, a 22…..a mn.
• Side diagonal consisting of elements a 1n , a 2n-1 .....a m1.

Main types of matrices:

• Square is a matrix where the number of rows = the number of columns ( m=n).
• Zero - where all matrix elements = 0.
• Transposed matrix - matrix IN, which was obtained from the original matrix A by replacing rows with columns.
• Unity - all elements of the main diagonal = 1, all others = 0.
• An inverse matrix is ​​a matrix that, when multiplied by the original matrix, results in an identity matrix.

The matrix can be symmetrical with respect to the main and secondary diagonals. That is, if a 12 = a 21, a 13 =a 31,….a 23 =a 32…. a m-1n =a mn-1, then the matrix is ​​symmetrical about the main diagonal. Only square matrices can be symmetric.

Methods for solving matrices.

Almost all matrix solving methods consist in finding its determinant n-th order and most of them are quite cumbersome. To find the determinant of the 2nd and 3rd order there are other, more rational methods.

Finding 2nd order determinants.

To calculate the determinant of a matrix A 2nd order, it is necessary to subtract the product of the elements of the secondary diagonal from the product of the elements of the main diagonal:

Methods for finding 3rd order determinants.

Below are the rules for finding the 3rd order determinant.

Simplified rule of triangle as one of matrix solving methods, can be depicted this way:

In other words, the product of elements in the first determinant that are connected by straight lines is taken with a “+” sign; Also, for the 2nd determinant, the corresponding products are taken with the “-” sign, that is, according to the following scheme:

At solving matrices using Sarrus' rule, to the right of the determinant, add the first 2 columns and the products of the corresponding elements on the main diagonal and on the diagonals that are parallel to it are taken with a “+” sign; and the products of the corresponding elements of the secondary diagonal and the diagonals that are parallel to it, with the sign “-”:

Decomposing the determinant in a row or column when solving matrices.

The determinant is equal to the sum of the products of the elements of the row of the determinant and their algebraic complements. Typically, the row/column that contains zeros is selected. The row or column along which the decomposition is carried out will be indicated by an arrow.

Reducing the determinant to triangular form when solving matrices.

At solving matrices method of reducing the determinant to a triangular form, they work like this: using the simplest transformations on rows or columns, the determinant becomes triangular in form and then its value, in accordance with the properties of the determinant, will be equal to the product of the elements that are on the main diagonal.

Laplace's theorem for solving matrices.

When solving matrices using Laplace's theorem, you need to know the theorem itself. Laplace's theorem: Let Δ - this is a determinant n-th order. We select any k rows (or columns), provided k≤ n - 1. In this case, the sum of the products of all minors k-th order contained in the selected k rows (columns), by their algebraic complements will be equal to the determinant.

Solving the inverse matrix.

Sequence of actions for inverse matrix solutions:

1. Determine whether a given matrix is ​​square. If the answer is negative, it becomes clear that there cannot be an inverse matrix for it.
2. We calculate algebraic complements.
3. We compose a union (mutual, adjoint) matrix C.
4. We compose the inverse matrix from algebraic additions: all elements of the adjoint matrix C divide by the determinant of the initial matrix. The final matrix will be the required inverse matrix relative to the given one.
5. We check the work done: multiply the initial matrix and the resulting matrix, the result should be an identity matrix.

Solving matrix systems.

For solutions of matrix systems The Gaussian method is most often used.

The Gauss method is a standard method for solving systems of linear algebraic equations(SLAE) and it lies in the fact that variables are sequentially eliminated, i.e., with the help of elementary changes, the system of equations is brought to an equivalent system of triangular form and from it, sequentially, starting from the last (by number), each element of the system is found.

Gauss method is the most versatile and the best tool to find the solution of the matrices. If a system has an infinite number of solutions or the system is incompatible, then it cannot be solved using Cramer’s rule and the matrix method.

The Gauss method also implies direct (reducing the extended matrix to a stepwise form, i.e., obtaining zeros under the main diagonal) and reverse (obtaining zeros above the main diagonal of the extended matrix) moves. The forward move is the Gauss method, the reverse move is the Gauss-Jordan method. The Gauss-Jordan method differs from the Gauss method only in the sequence of eliminating variables.

Let's consider system of linear algebraic equations(SLAU) relatively n unknown x 1 , x 2 , ..., x n :

This system in a “collapsed” form can be written as follows:

S n i=1 a ij x j = b i , i=1,2, ..., n.

In accordance with the matrix multiplication rule, the considered system of linear equations can be written in matrix form Ax=b, Where

, ,.

Matrix A, the columns of which are the coefficients for the corresponding unknowns, and the rows are the coefficients for the unknowns in the corresponding equation is called matrix of the system. Column matrix b, the elements of which are the right-hand sides of the equations of the system, is called the right-hand side matrix or simply right side of the system. Column matrix x , whose elements are the unknown unknowns, is called system solution.

A system of linear algebraic equations written in the form Ax=b, is matrix equation.

If the system matrix non-degenerate, then she has inverse matrix and then the solution to the system Ax=b is given by the formula:

x=A -1 b.

Example Solve the system matrix method.

Solution let's find the inverse matrix for the coefficient matrix of the system

Let's calculate the determinant by expanding along the first line:

Because the Δ ≠ 0 , That A -1 exists.

The inverse matrix was found correctly.

Let's find a solution to the system

Hence, x 1 = 1, x 2 = 2, x 3 = 3 .

Examination:

7. The Kronecker-Capelli theorem on the compatibility of a system of linear algebraic equations.

System of linear equations has the form:

a 21 x 1 + a 22 x 2 +... + a 2n x n = b 2, (5.1)

a m1 x 1 + a m1 x 2 +... + a mn x n = b m.

Here a i j and b i (i = ; j = ) are given, and x j are unknown real numbers. Using the concept of product of matrices, we can rewrite system (5.1) in the form:

where A = (a i j) is a matrix consisting of coefficients for the unknowns of system (5.1), which is called matrix of the system, X = (x 1 , x 2 ,..., x n) T , B = (b 1 , b 2 ,..., b m) T are column vectors composed respectively of unknowns x j and free terms b i .

Ordered collection n real numbers (c 1, c 2,..., c n) is called system solution(5.1), if as a result of substituting these numbers instead of the corresponding variables x 1, x 2,..., x n, each equation of the system turns into an arithmetic identity; in other words, if there is a vector C= (c 1 , c 2 ,..., c n) T such that AC  B.

System (5.1) is called joint, or solvable, if it has at least one solution. The system is called incompatible, or unsolvable, if it has no solutions.

,

formed by assigning a column of free terms to the matrix A on the right is called extended matrix of the system.

The question of compatibility of system (5.1) is solved by the following theorem.

Kronecker-Capelli theorem . A system of linear equations is consistent if and only if the ranks of matrices A andA coincide, i.e. r(A) = r(A) = r.

For the set M of solutions of system (5.1) there are three possibilities:

1) M =  (in this case the system is inconsistent);

2) M consists of one element, i.e. the system has a unique solution (in this case the system is called certain);

3) M consists of more than one element (then the system is called uncertain). In the third case, system (5.1) has an infinite number of solutions.

The system has a unique solution only if r(A) = n. In this case, the number of equations is not less than the number of unknowns (mn); if m>n, then m-n equations are consequences of the others. If 0

To solve an arbitrary system of linear equations, you need to be able to solve systems in which the number of equations is equal to the number of unknowns - the so-called Cramer type systems:

a 11 x 1 + a 12 x 2 +... + a 1n x n = b 1,

a 21 x 1 + a 22 x 2 +... + a 2n x n = b 2, (5.3)

... ... ... ... ... ...

a n1 x 1 + a n1 x 2 +... + a nn x n = b n .

Systems (5.3) are solved in one of the following ways: 1) the Gauss method, or the method of eliminating unknowns; 2) according to Cramer's formulas; 3) matrix method.

Example 2.12. Explore the system of equations and solve it if it is consistent:

5x 1 - x 2 + 2x 3 + x 4 = 7,

2x 1 + x 2 + 4x 3 - 2x 4 = 1,

x 1 - 3x 2 - 6x 3 + 5x 4 = 0.

Solution. We write out the extended matrix of the system:

 .

Let's calculate the rank of the main matrix of the system. It is obvious that, for example, the second-order minor in the upper left corner = 7  0; the third-order minors containing it are equal to zero:

Consequently, the rank of the main matrix of the system is 2, i.e. r(A) = 2. To calculate the rank of the extended matrix A, consider the bordering minor

this means that the rank of the extended matrix r(A) = 3. Since r(A)  r(A), the system is inconsistent.

Equations in general, linear algebraic equations and their systems, as well as methods for solving them, occupy a special place in mathematics, both theoretical and applied.

This is due to the fact that the vast majority of physical, economic, technical and even pedagogical problems can be described and solved using a variety of equations and their systems. Recently, mathematical modeling has gained particular popularity among researchers, scientists and practitioners in almost all subject areas, which is explained by its obvious advantages over other well-known and proven methods for studying objects of various natures, in particular, the so-called complex systems. There is a great variety of different definitions of a mathematical model given by scientists at different times, but in our opinion, the most successful is the following statement. A mathematical model is an idea expressed by an equation. Thus, the ability to compose and solve equations and their systems is an integral characteristic of a modern specialist.

To solve systems of linear algebraic equations, the most commonly used methods are Cramer, Jordan-Gauss and the matrix method.

Matrix solution method is a method for solving systems of linear algebraic equations with a nonzero determinant using an inverse matrix.

If we write out the coefficients for the unknown quantities xi in matrix A, collect the unknown quantities in the vector column X, and the free terms in the vector column B, then the system of linear algebraic equations can be written in the form of the following matrix equation A · X = B, which has a unique solution only when the determinant of matrix A is not equal to zero. In this case, the solution to the system of equations can be found in the following way X = A-1 · B, Where A-1 is the inverse matrix.

The matrix solution method is as follows.

Let us be given a system of linear equations with n unknown:

It can be rewritten in matrix form: AX = B, Where A- the main matrix of the system, B And X- columns of free terms and solutions of the system, respectively:

Let's multiply this matrix equation from the left by A-1 - matrix inverse of matrix A: A -1 (AX) = A -1 B

Because A -1 A = E, we get X= A -1 B. The right side of this equation will give the solution column of the original system. The condition for the applicability of this method (as well as the general existence of a solution to an inhomogeneous system of linear equations with the number of equations equal to the number of unknowns) is the nondegeneracy of the matrix A. A necessary and sufficient condition for this is that the determinant of the matrix is ​​not equal to zero A:det A≠ 0.

For a homogeneous system of linear equations, that is, when the vector B = 0 , indeed the opposite rule: the system AX = 0 has a non-trivial (that is, non-zero) solution only if det A= 0. Such a connection between solutions of homogeneous and inhomogeneous systems of linear equations is called the Fredholm alternative.

Example solutions to an inhomogeneous system of linear algebraic equations.

Let us make sure that the determinant of the matrix, composed of the coefficients of the unknowns of the system of linear algebraic equations, is not equal to zero.

The next step is to calculate the algebraic complements for the elements of the matrix consisting of the coefficients of the unknowns. They will be needed to find the inverse matrix.