Тест Тьюринга, предложенный Аланом Тьюрингом , был разработан в качестве удовлетворительного функционального определения интеллекта. Тьюринг решил, что нет смысла разрабатывать обширный список требований, необходимых для создания искусственного интеллекта, который к тому же может оказаться противоречивым, и предложил тест, основанный на том, что поведение объекта, обладающего искусственным интеллектом, в конечном итоге нельзя будет отличить от поведения таких бесспорно интеллектуальных сущностей, как человеческие существа. Компьютер успешно пройдет этот тест, если человек-экспериментатор, задавший ему в письменном виде определенные вопросы, не сможет определить, получены ли письменные ответы от другого человека или от некоторого устройства.

Решение задачи по составлению программы для компьютера для того, чтобы он прошел этот тест, требует большого объема работы. Запрограммированный таким образом компьютер должен обладать перечисленными ниже возможностями:

• Средства обработки текстов на естественных языках (Natural Language Processing - NLP), позволяющие успешно общаться с компьютером, скажем на английском языке.
• Средства представления знаний , с помощью которых компьютер может записать в память то, что он узнает или прочитает.
• Средства автоматического формирования логических выводов , обеспечивающие возможность использовать хранимую информацию для поиска ответов на вопросы и вывода новых заключений.
• Средства машинного обучения , которые позволяют приспосабливаться к новым обстоятельствам, а также обнаруживать и экстраполировать признаки стандартных ситуаций.

В тесте Тьюринга сознательно исключено непосредственное физическое взаимодействие экспериментатора и компьютера, поскольку для создания искусственного интеллекта не требуется физическая имитация человека. Но в так называемом полном тесте Тьюринга предусмотрено использование видеосигнала для того, чтобы экспериментатор мог проверить способности испытуемого объекта к восприятию, а также имел возможность представить физические объекты "в неполном виде" (пропустить их "через штриховку"). Чтобы пройти полный тест Тьюринга, компьютер должен обладать перечисленными ниже способностями:

• Машинное зрение для восприятия объектов.
• Средства робототехники для манипулирования объектами и перемещения в пространстве.

Шесть направлений исследований, перечисленных в данном разделе, составляют основную часть искусственного интеллекта, а Тьюринг заслуживает нашей благодарности за то, что предложил такой тест, который не потерял своей значимости и через 50 лет. Тем не менее исследователи искусственного интеллекта практически не занимаются решением задачи прохождения теста Тьюринга, считая, что гораздо важнее изучить основополагающие принципы интеллекта, чем продублировать одного из носителей естественного интеллекта. В частности, проблему "искусственного полета" удалось успешно решить лишь после того, как братья Райт и другие исследователи перестали имитировать птиц и приступили к изучению аэродинамики. В научных и технических работах по воздухоплаванию цель этой области знаний не определяется как "создание машин, которые в своем полете настолько напоминают голубей, что даже могут обмануть настоящих птиц".

Тема “Машина Тьюринга” в школьном курсе информатики

И.Н. Фалина,
Москва

Во многих учебниках по информатике при изучении понятия и свойств алгоритма присутствуют фразы такого содержания: “…существует много разных способов для записи одного и того же алгоритма, например, запись в виде текста, запись в виде блок-схемы, запись на каком-либо алгоритмическом языке, представление алгоритма в виде машины Тьюринга или машины Поста…”. К сожалению, такого типа фразы являются единственными, где упоминается машина Тьюринга. Без сомнения, объем часов, отводимых на изучение алгоритмов, не позволяет включать в эту тему еще и изучение способов записи алгоритма в виде машины Тьюринга. Но эта тема крайне интересна, важна и полезна для школьников, особенно увлекающихся информатикой.

Тема “Машина Тьюринга” может изучаться в 8–11-х классах в рамках темы “Информационные процессы. Обработка информации”, на факультативных занятиях, в системе дополнительного образования, например, в школах юных программистов. Изучение этой темы может сопровождаться компьютерной поддержкой, если у учителя есть программный тренажер-имитатор “Машина Тьюринга”. В классах с углубленным изучением программирования школьники могут самостоятельно написать программу “Машина Тьюринга”. В рамках этой статьи вашему вниманию предлагается практикум по решению задач на тему “Машина Тьюринга”. Теоретический материал по данной теме не раз печатался на страницах газеты “Информатика”, например, в № 3/2004 статья И.Н. Фалиной “Элементы теории алгоритмов”.

Машина Тьюринга - это строгое математическое построение, математический аппарат (аналогичный, например, аппарату дифференциальных уравнений), созданный для решения определенных задач. Этот математический аппарат был назван “машиной” по той причине, что по описанию его составляющих частей и функционированию он похож на вычислительную машину. Принципиальное отличие машины Тьюринга от вычислительных машин состоит в том, что ее запоминающее устройство представляет собой бесконечную ленту: у реальных вычислительных машин запоминающее устройство может быть как угодно большим, но обязательно конечным. Машину Тьюринга нельзя реализовать именно из-за бесконечности ее ленты. В этом смысле она мощнее любой вычислительной машины.

В каждой машине Тьюринга есть две части:

1) неограниченная в обе стороны лента , разделенная на ячейки;

2) автомат (головка для считывания/записи, управляемая программой).

С каждой машиной Тьюринга связаны два конечных алфавита : алфавит входных символов A = {a 0 , a 1 , ..., a m }и алфавит состояний Q = {q 0 , q 1 , ..., q p }. (С разными машинами Тьюринга могут быть связаны разные алфавиты A и Q .) Состояние q 0 называется пассивным . Считается, что если машина попала в это состояние, то она закончила свою работу. Состояние q 1 называется начальным . Находясь в этом состоянии, машина начинает свою работу.

Входное слово размещается на ленте по одной букве в расположенных подряд ячейках. Слева и справа от входного слова находятся только пустые ячейки (в алфавит А всегда входит пустая буква а 0 - признак того, что ячейка пуста).

Автомат может двигаться вдоль ленты влево или вправо, читать содержимое ячеек и записывать в ячейки буквы. Ниже схематично нарисована машина Тьюринга, автомат которой обозревает первую ячейку с данными.

Автомат каждый раз “видит” только одну ячейку. В зависимости от того, какую букву ai он видит, а также в зависимости от своего состояния qj автомат может выполнять следующие действия:

• · записать новую букву в обозреваемую ячейку;
• · выполнить сдвиг по ленте на одну ячейку вправо/влево или остаться неподвижным;
• · перейти в новое состояние.

То есть у машины Тьюринга есть три вида операций. Каждый раз для очередной пары (q j , a i ) машина Тьюринга выполняет команду, состоящую из трех операций с определенными параметрами.

Программа для машины Тьюринга представляет собой таблицу, в каждой клетке которой записана команда.

Клетка (q j , a i ) определяется двумя параметрами - символом алфавита и состоянием машины. Команда представляет собой указание: куда передвинуть головку чтения/записи, какой символ записать в текущую ячейку, в какое состояние перейти машине. Для обозначения направления движения автомата используем одну из трех букв: “Л” (влево), “П” (вправо) или “Н” (неподвижен).

После выполнения автоматом очередной команды он переходит в состояние q m (которое может в частном случае совпадать с прежним состоянием q j ). Следующую команду нужно искать в m -й строке таблицы на пересечении со столбцом a l (букву a l автомат видит после сдвига).

Договоримся, что когда лента содержит входное слово, то автомат находится против какой-то ячейки в состоянии q 1. В процессе работы автомат будет перескакивать из одной клетки программы (таблицы) в другую, пока не дойдет до клетки, в которой записано, что автомат должен перейти в состояние q 0 . Эти клетки называются клетками останова . Дойдя до любой такой клетки, машина Тьюринга останавливается .

Несмотря на свое простое устройство, машина Тьюринга может выполнять все возможные преобразования слов, реализуя тем самым все возможные алгоритмы.

Пример. Требуется построить машину Тьюринга, которая прибавляет единицу к числу на ленте. Входное слово состоит из цифр целого десятичного числа, записанных в последовательные ячейки на ленте. В начальный момент машина находится против самой правой цифры числа.

Решение. Машина должна прибавить единицу к последней цифре числа. Если последняя цифра равна 9, то ее заменить на 0 и прибавить единицу к предыдущей цифре. Программа для данной машины Тьюринга может выглядеть так:

В этой машине Тьюринга q 1 - состояние изменения цифры, q 0 - состояние останова. Если в состоянии q l автомат видит цифру 0..8, то он заменяет ее на 1..9 соответственно и переходит в состояние q 0 , т.е. машина останавливается. Если же он видит цифру 9, то заменяет ее на 0, сдвигается влево, оставаясь в состоянии q l . Так продолжается до тех пор, пока автомат не встретит цифру меньше 9. Если же все цифры были равны 9, то он заменит их нулями, запишет 0 на месте старшей цифры, сдвинется влево и в пустой клетке запишет 1. Затем перейдет в состояние q 0 , т.е. остановится.

Практические задания

1. На ленте машины Тьюринга содержится последовательность символов “+”. Напишите программу для машины Тьюринга, которая каждый второй символ “+” заменит на “–”. Замена начинается с правого конца последовательности. Автомат в состоянии q 1 обозревает один из символов указанной последовательности. Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.

2. Дано число n в восьмеричной системе счисления. Разработать машину Тьюринга, которая увеличивала бы заданное число n на 1. Автомат в состоянии q 1 обозревает некую цифру входного слова. Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.

3. Дана десятичная запись натурального числа n > 1. Разработать машину Тьюринга, которая уменьшала бы заданное число n на 1. Автомат в состоянии q 1 обозревает правую цифру числа. Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.

4. Дано натуральное число n > 1. Разработать машину Тьюринга, которая уменьшала бы заданное число n на 1, при этом в выходном слове старшая цифра не должна быть 0. Например, если входным словом было “100”, то выходным словом должно быть “99”, а не “099”. Автомат в состоянии q 1 обозревает правую цифру числа. Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.

5. Дан массив из открывающих и закрывающих скобок. Построить машину Тьюринга, которая удаляла бы пары взаимных скобок, т.е. расположенных подряд “()”.

Например, дано “) (() (()”, надо получить “) . . . ((”.

Автомат в состоянии q

6. Дана строка из букв “a ” и “b ”. Разработать машину Тьюринга, которая переместит все буквы “a ” в левую, а буквы “b ” - в правую части строки. Автомат в состоянии q 1 обозревает крайний левый символ строки. Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.

7. На ленте машины Тьюринга находится число, записанное в десятичной системе счисления. Умножить это число на 2. Автомат в состоянии q 1 обозревает крайнюю левую цифру числа. Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.

8. Даны два натуральных числа m и n , представленные в унарной системе счисления. Соответствующие наборы символов “|” разделены пустой клеткой. Автомат в состоянии q 1 обозревает самый правый символ входной последовательности. Разработать машину Тьюринга, которая на ленте оставит сумму чисел m и n . Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.

9. Даны два натуральных числа m и n , представленных в унарной системе счисления. Соответствующие наборы символов “|” разделены пустой клеткой. Автомат в состоянии q 1 обозревает самый правый символ входной последовательности. Разработать машину Тьюринга, которая на ленте оставит разность чисел m и n . Известно, что m > n . Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.

10. На ленте машины Тьюринга находится десятичное число. Определить, делится ли это число на 5 без остатка. Если делится, то записать справа от числа слово “да”, иначе - “нет”. Автомат обозревает некую цифру входного числа. Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.

В состоянии q 1 машина ищет правый конец числа, в состоянии q 2 - пропускает знак “+”, при достижении конца последовательности - останавливается. В состоянии q 3 машина знак “+” заменяет на знак “–”, при достижении конца последовательности она останавливается.

Решение этой задачи аналогично рассмотренному выше примеру.

Состояние q 1 - уменьшаем младшую (очередную) цифру на 1. Если она не равна нулю, то после уменьшения сразу - останов, если же младшая цифра равна 0, то вместо нее пишем 9, смещаемся влево и вновь выполняем вычитание. В клетку [a 0 , q 1 ] машина Тьюринга никогда не попадет, поэтому ее можно не заполнять.

Задача 4 (усложнение задачи 3)

Состояние q 1 - уменьшаем младшую (очередную) цифру на 1. Если она больше 1, то после уменьшения - сразу останов, если же младшая цифра равна 0, то вместо нее пишем 9, смещаемся влево и вновь выполняем вычитание. Если уменьшаемая цифра равна 1, то вместо нее пишем 0 и переходим в состояние q 2 .

Состояние q 2 - после записи “0” в каком-либо разряде надо проанализировать, не является ли этот ноль старшей незначащей цифрой (т.е. не стоит ли слева от него в записи выходного слова a 0).

Состояние q 3 - если записанный “0” является старшей незначащей цифрой, то его надо удалить из записи выходного слова.

Те клетки, в которые машина Тьюринга никогда не попадает, оставляем пустыми.

Состояние q 1: если встретили “(”, то сдвиг вправо и переход в состояние q 2 ; если встретили “a 0 ”, то останов.

Состояние q 2: анализ символа “(” на парность, в случае парности должны увидеть “)”. Если парная, то возврат влево и переход в состояние q 3 .

Состояние q 3: стираем сначала “(”, затем “)” и переходим в q 1 .

Решение этой задачи обычно вызывает у школьников затруднение. При разборе решения этой задачи можно пойти, например, следующим путем.

Рассмотрите со школьниками следующие варианты входных слов и попросите их сформулировать, что должна делать машина Тьюринга, каков внешний вид выходного слова, чем с точки зрения машины Тьюринга эти варианты различаются:

aaa ->

a -> выходное слово совпадает с входным, просматриваем входное слово до тех пор, пока оно не заканчивается.

bbb -> выходное слово совпадает с входным, просматриваем входное слово до тех пор, пока оно не заканчивается.

b -> выходное слово совпадает с входным, просматриваем входное слово до тех пор, пока оно не заканчивается.

ab -> выходное слово совпадает с входным, просматриваем входное слово до тех пор, пока оно не заканчивается.

Результат обсуждения. Машина Тьюринга должна “понимать”, по цепочке каких букв она идет, т.е. у нее должно быть как минимум два состояния. Пусть состояние q 1 - движение по цепочке из букв “a ”, а q 2 - состояние движения по цепочке из букв “b ”. Заметим, что цепочка может состоять и из одной буквы. Если мы дошли до конца строки в состоянии q 1 или q 2 , т.е. встретили a 0 , машина должна остановиться, мы обработали всю строку.

Рассмотрим следующие варианты входных слов:

bba -> abb

bbbaab -> aabbbb

aabbbaab -> aaaabbbb

Результат обсуждения. Первый вариант входного слова можно последовательно обработать следующим образом: bba -> bbb -> вернуться к левому концу цепочки из букв “b ” -> abb (заменить первую букву в этой цепочке на “a ”). Для выполнения этих действий нам потребуется ввести два новых состояния и, кроме того, уточнить состояние q 2 . Таким образом, для решения этой задачи нам нужно построить машину Тьюринга со следующими состояниями:

q 1 - идем вправо по цепочке букв “a ”. Если цепочка заканчивается a 0 , то переходим в q 0 ; если заканчивается буквой “b ”, то переходим в q 2 ;

q 2 - идем вправо по цепочке букв “b ”, если цепочка заканчивается a 0 , то переходим в q 0 ; если заканчивается “a ”, то заменяем букву “a ” на “b ”, переходим в состояние q 3 (цепочку вида заменили на цепочку вида );

q 3 - идем влево по цепочке букв “b ” до ее левого конца. Если встретили a 0 или “a ”, то переходим в q 4 ;

q 4 - заменяем “b ” на “a ” и переходим в q 1 (цепочку вида заменяем на цепочку вида .

Задача 7

состояние q 1 - поиск правой (младшей) цифры числа;

состояние q 2 -умножение очередной цифры числа на 2 без прибавления 1 переноса;

состояние q 3 - умножение очередной цифры числа на 2 с прибавлением 1 переноса.

Машина Тьюринга для этой программы выглядит тривиально просто - в ней всего одно состояние. Такая машина Тьюринга выполняет следующие действия: стирает самый правый штрих, ищет разделитель (пустую ячейку) и в эту пустую ячейку помещает штрих, тем самым сформирована непрерывная последовательность штрихов длины n + m .

Однако, как ни странно, решение этой задачи вызывает большие трудности. Очень часто ученики строят машину Тьюринга, которая выполняет циклические действия: последовательно пододвигают правые n штрихов к левым.

В этом случае их программа выглядит следующим образом:

состояние q 1 -поиск разделителя;

состояние q 2 -передвинули штрих;

состояние q 3 -проверка на конец (все ли штрихи передвинули).

На примере этой задачи четко видно, как часто дети пытаются решить задачу уже знакомыми способами. Мне кажется, что, предлагая ученикам задачи на составление машин Тьюринга, мы развиваем способность к нахождению необычных решений, развиваем способность творчески думать!

Эта задача кажется школьникам достаточно легкой, но трудности возникают с остановом машины Тьюринга. Ниже приведен один из возможных вариантов машины Тьюринга для этой задачи.

Идея решения (условие останова). На ленте есть два исходных массива штрихов.

Штрихи начинаем стирать с левого конца массива m . И поочередно стираем самый левый штрих в массиве m и самый правый штрих в массиве n . Но прежде чем стереть правый штрих в массиве n , проверяем, единственный он (т.е. последний, который надо стереть) или нет.

Опишем сначала состояния машины Тьюринга, которые необходимы для решения нашей задачи, а затем составим программу-таблицу.

Состояние q 1 - поиск разделителя между массивами штрихов при движении справа налево;

состояние q 2 - поиск левого штриха в массиве m ;

состояние q 3 - удаление левого штриха в массиве m ;

состояние q 4 - поиск разделителя при движении слева направо;

состояние q 5 - поиск правого штриха в массиве n ;

состояние q 6 - проверка единственности этого штриха в массиве n , т.е. определяем, был ли он последним;

состояние q 7 - если он был последним, то останов, иначе переход на новый цикл выполнения алгоритма.

При решении этой задачи следует обратить внимание на правильное выписывание алфавита:

A = {a 0 , 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, Д, А, Н, Е, Т}.

Состояние q 1 -поиск правого конца числа;

состояние q 2 -анализ младшей цифры числа; если она равна “0” или “5”, т.е. число делится на 5, то переход в состояние q 3 , иначе переход в состояние q 5 ;

состояние q 3 -запись буквы “Д” справа от слова на ленте;

состояние q 4 -запись буквы “А” справа от слова и останов машины;

состояние q 5 -запись буквы “Н” справа от слова;

состояние q 6 -запись буквы “Е” справа от слова;

состояние q 7 -запись буквы “Т” справа от слова и останов машины.

Свойства машины Тьюринга как алгоритма

На примере машины Тьюринга хорошо прослеживаются свойства алгоритмов. Попросите учащихся показать, что машина Тьюринга обладает всеми свойствами алгоритма.

Дискретность. Машина Тьюринга может перейти к (к + 1)-му шагу только после выполнения к- го шага, т.к. именно к- й шаг определяет, каким будет (к + 1)-й шаг.

Понятность. На каждом шаге в ячейку пишется символ из алфавита, автомат делает одно движение (Л, П, Н), и машина Тьюринга переходит в одно из описанных состояний.

Детерминированность. В каждой клетке таблицы машины Тьюринга записан лишь один вариант действия. На каждом шаге результат определен однозначно, следовательно, последовательность шагов решения задачи определена однозначно, т.е. если машине Тьюринга на вход подают одно и то же входное слово, то выходное слово каждый раз будет одним и тем же.

Результативность. Содержательно результаты каждого шага и всей последовательности шагов определены однозначно, следовательно, правильно написанная машина Тьюринга за конечное число шагов перейдет в состояние q 0, т.е. за конечное число шагов будет получен ответ на вопрос задачи.

Массовость. Каждая машина Тьюринга определена над всеми допустимыми словами из алфавита, в этом и состоит свойство массовости. Каждая машина Тьюринга предназначена для решения одного класса задач, т.е. для каждой задачи пишется своя (новая) машина Тьюринга.

ОТ РЕДАКЦИИ

Все приведенные в статье задачи можно решить просто в тетради, начертив информационную ленту и программу-таблицу. Но можно сделать этот процесс более увлекательным и наглядным: воспользоваться машинной реализацией - интерпретатором машины Поста и машины Тьюринга “Algo2000”, созданным Радиком Зартдиновым. Программа обладает интуитивно понятным интерфейсом, и требования у нее самые умеренные: компьютер IBM PC AT 486 и выше, наличие операционной системы Windows"95/98/NT.

Посмотрим в общих чертах, как работает “Algo2000”.

В меню программы выберем пункт Интерпретатор и укажем, с какой машиной мы хотим работать (в нашем случае это “машина Тьюринга”).

Перед нами появится поле машины Тьюринга.

Теперь необходимо задать внешний алфавит, т.е. в строке Внешний алфавит указать, какие символы в него входят (если строка Внешний алфавит не видна, нужно выбрать пункт меню Вид | Внешний алфавит ). Каждый символ можно указать только один раз. После окончания ввода внешнего алфавита формируется первый столбец таблицы: он заполняется символами внешнего алфавита в том же порядке. При редактировании внешнего алфавита автоматически изменяется таблица: вставляются, удаляются или меняются местами строки.

Не забудем, что нужно как-то расставить символы внешнего алфавита по секциям ленты (можно все секции оставить пустыми) и поставить каретку против одной из секций, т.е. надо задать программу и некоторое состояние машины.

Теперь можно приступить непосредственно к записи алгоритма решения задачи. Он задается в виде таблицы: в каждый столбец верхней строчки заносятся символы внутреннего алфавита, в каждую строчку первого столбца - символы внешнего алфавита. В ячейках на пересечении других столбцов и строчек помещаются команды. Если на пересечении какой-либо строки и какого-либо столбца мы получим пустую клетку, то это означает, что в данном внутреннем состоянии данный символ встретиться не может.

Например, мы составляем алгоритм нахождения разности двух целых положительных чисел (в десятичной системе счисления), если известно, что первое число больше второго, а между ними стоит знак минус.

Поле программы будет выглядеть так:

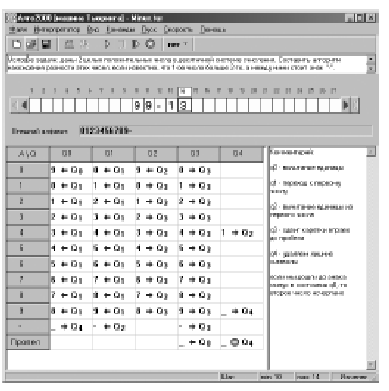
Формат команды в каждой ячейке - aKq. Здесь:
a - новое содержание текущей ячейки (новый символ внешнего алфавита, который заносится в текущую ячейку), K - команда лентопротяжного механизма машины Тьюринга (влево, вправо, стоп), q - новое внутреннее состояние машины Тьюринга.

Кнопка запустит программу. Если выполнение не было приостановлено, то оно всегда начинается с нулевого внутреннего состояния Q0.

Программу можно выполнить по шагам. Для этого нажмите на кнопку на панели инструментов (если кнопки не видны, нужно выбрать пункт меню Вид | Панель инструментов ) или выберите в главном меню Пуск | Пошагово . Если необходимо полностью прервать выполнение программы, то это можно сделать с помощью кнопки на панели инструментов или с помощью главного меню (Пуск | Прервать ). Пункт меню Скорость позволяет регулировать скорость выполнения программы.

Выполнение программы будет идти до тех пор, пока не встретится команда “Стоп” или не возникнет какая-нибудь ошибка.

При возникновении вопросов в ходе работы с программой-интерпретатором обращайтесь к справочному файлу Algo2000.hlp . Его, так же, как и саму программу “Algo2000”, можно найти на сайте газеты “Информатика” http://inf.1september.ru в разделе “Download”.

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ» Т.К. Кацаран, Л.Н. Строева МАШИНА ТЬЮРИНГА И РЕКУРСИВНЫЕ ФУНКЦИИ Учебное пособие для вузов Издательско-полиграфический центр Воронежского государственного университета 2008 Утверждено научно-методическим советом факультета ПММ 25 мая 2008 г., протокол № 9 Рецензент д. т. н., проф. кафедры математических методов исследования операций Т.М. Леденева Учебное пособие подготовлено на кафедре нелинейных колебаний факуль- тета ПММ Воронежского государственного университета. Рекомендуется для студентов 1 курса факультета ПММ ВГУ, Староосколь- ского и Лискинского филиалов ВГУ. Для специальности 010500 – Прикладная математика и информатика ВВЕДЕНИЕ Слово «алгоритм» происходит от algorithmi – латинского написания имени узбекского математика и астронома, жившего в VIII–IX веках (783– 850 гг.), Мухаммеда бен Мусы аль-Хорезми. Под этим именем в Средневе- ковой Европе знали величайшего математика из Хорезма (город в совре- менном Узбекистане). В своей книге «Об индийском счете» он сформули- ровал правила записи натуральных чисел с помощью арабских цифр и пра- вила действий над ними. Затем понятие алгоритма стало использоваться в более широком смысле и не только в математике. Как для математиков, так и для практиков понятие алгоритма имеет важное значение. Таким образом, можно сказать, что алгоритм – это точное предписа- ние о выполнении в определенном порядке некоторой системы операций для решения всех задач одного и того же типа, определяющее последова- тельность действий, обеспечивающую получение требуемого результата из исходных данных. Заметим, что это не определение понятия «алгоритм», а только его описание, его интуитивный смысл. Алгоритм может быть предназначен для выполнения его как челове- ком, так и автоматическим устройством. Данное представление об алгоритме не является строгим с матема- тической точки зрения, так как в нем используются такие понятия как «точное предписание» и «исходные данные», которые, вообще говоря, строго не определены. Особенностью любого алгоритма является его способность решать некоторый класс задач. Например, это может быть алгоритм решения сис- тем линейных уравнений, нахождение кратчайшего пути в графе и т. д. Создание алгоритма, пусть даже самого простого, – процесс твор- ческий. Он доступен исключительно живым существам, а долгое время считалось, что только человеку. Другое дело – реализация уже имеюще- 3 гося алгоритма. Ее можно поручить субъекту или объекту, который не обязан вникать в сущность дела, а возможно, и не способен его понять. Такой субъект или объект принято называть формальным исполнителем. Примером формального исполнителя может служить стиральная маши- на-автомат, которая неукоснительно исполняет предписанные ей дейст- вия, даже если вы забыли положить в нее порошок. Человек тоже может выступать в роли формального исполнителя, но в первую очередь фор- мальными исполнителями являются различные автоматические устрой- ства, и компьютер в том числе. Каждый алгоритм создается в расчете на вполне конкретного исполнителя. Те действия, которые может совер- шать исполнитель, называются его допустимыми действиями. Совокуп- ность допустимых действий образует систему команд исполнителя. Ал- горитм должен содержать только те действия, которые допустимы для данного исполнителя. Поэтому обычно формулируют несколько общих свойств алгорит- мов, позволяющих отличать алгоритмы от других инструкций. Алгоритм должен обладать следующими свойствами. Дискретность (прерывность, раздельность) – алгоритм должен представлять процесс решения задачи как последовательное выполнение простых (или ранее определенных) шагов. Каждое действие, предусмот- ренное алгоритмом, исполняется только после того, как закончилось ис- полнение предыдущего. Определенность – каждое правило алгоритма должно быть четким, однозначным и не оставлять места для произвола. Благодаря этому свойст- ву выполнение алгоритма носит механический характер и не требует ника- ких дополнительных указаний или сведений о решаемой задаче. Результативность (конечность) – алгоритм должен приводить к ре- шению задачи за конечное число шагов. 4 Массовость – алгоритм решения задачи разрабатывается в общем виде, то есть, он должен быть применим для некоторого класса задач, раз- личающихся только исходными данными. При этом исходные данные мо- гут выбираться из некоторой области, которая называется областью при- менимости алгоритма. Теория алгоритмов – это раздел математики, который изучает общие свойства алгоритмов. Различают качественную и метрическую теорию ал- горитмов. Основной проблемой качественной теории алгоритмов является про- блема построения алгоритма, обладающего заданными свойствами. Такую проблему называют алгоритмической. Метрическая теория алгоритмов исследует алгоритм с точки зрения их сложности. Этот раздел теории алгоритмов известен также как алго- ритмическая теория сложности. При отыскании решений некоторых задач долго не удавалось най- ти соответствующий алгоритм. Примерами таких задач являются: а) ука- зать способ, согласно которому для любой предикатной формулы за ко- нечное число действий можно выяснить, является ли она тождественно- истинной или нет; б) разрешимо ли в целых числах диофантово уравне- ние (алгебраическое уравнение с целыми коэффициентами). Так как для решения этих задач найти алгоритмов не удалось, возникло предполо- жение, что такие алгоритмы вообще не существуют, что и доказано: первая задача решена А. Черчем, а вторая – Ю.В. Матиясевичем и Г.В. Чудновским. Доказать это с помощью интуитивного понятия алго- ритма в принципе невозможно. Поэтому были предприняты попытки дать точное математическое определение понятия алгоритма. В середине 30-х годов ХХ века С.К. Клини, А.А. Марков, Э. Пост, А. Тьюринг, А. Черч и другие предположили различные математические определения 5 понятия алгоритма. Впоследствии было доказано, что эти различные формальные математические определения в некотором смысле эквива- ленты: вычисляют одно и то же множество функций. Это говорит о том, что, по-видимому, основные черты интуитивного понятия алгоритма правильно отражены в этих определениях. Далее рассмотрим математическое уточнение алгоритма, предло- женное А. Тьюрингом, которое называют машиной Тьюринга. 6 1. МАШИНА ТЬЮРИНГА § 1. Математическая модель машины Тьюринга Идея создания машины Тьюринга, предложенная английским мате- матиком А. Тьюрингом в тридцатых годах XX века, связана с его попыт- кой дать точное математическое определение понятия алгоритма. Машина Тьюринга (МТ) – это математическая модель идеализиро- ванной цифровой вычислительной машины. Машина Тьюринга является таким же математическим объектом, как функция, производная, интеграл, группа и т. д. Так же как и другие мате- матические понятия, понятие машины Тьюринга отражает объективную реальность, моделирует некие реальные процессы. Для описания алгоритма МТ удобно представлять некоторое устрой- ство, состоящее из четырех частей: ленты, считывающей головки, устрой- ства управления и внутренней памяти. 1. Лента предполагается потенциально бесконечной, разбитой на ячейки (равные клетки). При необходимости к первой или последней клет- ке, в которой находятся символы пристраивается пустая клетка. Машина работает во времени, которое считается дискретным, и его моменты зану- мерованы 1, 2, 3, … . В каждый момент лента содержит конечное число клеток. В клетки в дискретный момент времени может быть записан толь- ко один символ (буква) из внешнего алфавита A = {L, a1 , a 2 ,..., a n -1 }, n ³ 2 . Пустая ячейка обозначается символом L, а сам символ L называется пустым, при этом остальные символы называются непустыми. В этом ал- фавите A в виде слова (конечного упорядоченного набора символов) ко- дируется та информация, которая подается в МТ. Машина «перерабатыва- ет» информацию, поданную в виде слова, в новое слово. 2. Считывающая головка (некоторый считывающий элемент) пере- мещается вдоль ленты так, что в каждый момент времени она обозревает 7 ровно одну ячейку ленты. Головка может считывать содержимое ячейки и записывать в нее новый символ из алфавита А. В одном такте работы она может сдвигаться только на одну ячейку вправо (П), влево (Л) или оста- ваться на месте (Н). Обозначим множество перемещений (сдвига) головки D = {П, Л, Н}. Если в данный момент времени t головка находится в край- ней клетке и сдвигается в отсутствующую клетку, то пристраивается новая пустая клетка, над которой окажется головка в момент t + 1 . 3. Внутренняя память машины представляет собой некоторое конеч- ное множество внутренних состояний Q = { q0 , q1 , q 2 , ..., q m }, m ³ 1 . Бу- дем считать, что мощность |Q | ³ 2. Два состояния машины имеют особое значение: q1 – начальное внутреннее состояние (начальных внутренних состояний может быть несколько), q0 – заключительное состояние или стоп-состояние (заключительное состояние всегда одно). В каждый момент времени МТ характеризуется положением головки и внутренним состоя- нием. Например, под ячейкой, над которой находится головка, указывается внутреннее состояние машины. ¯ a2 a1 L a2 a3 q1 4. Устройство управления в каждый момент t в зависимости от счи- тываемого в этот момент символа на ленте и внутреннего состояния ма- шины выполняет следующие действия: 1) изменяет считываемый в момент t символ ai на новый символ a j (в частности оставляет его без изменений, т. е. ai = a j); 2) передвигает головку в одном из следующих направлений: Н, Л, П; 3) изменяет имеющееся в момент t внутреннее состояние машины 8 qi на новое q j , в котором будет машина в момент времени t +1 (может быть, что qi = q j). Такие действия устройства управления называют командой, которую можно записать в виде: qi ai ® a j D q j , (1) где qi – внутреннее состояние машины в данный момент; a i – считываемый в этот момент символ; a j – символ, на который изменяется символ a i (может быть ai = a j); символ D есть или Н, или Л, или П и указывает направление движения головки; q j – внутреннее состояние машины в следующий момент (может быть qi = q j). Выражения qi ai и a j D q j называются левой и правой частями этой команды соответственно. Число команд, в которых левые части попарно различ- ны, является конечным числом, так как множества Q \ {q 0 } и A конечны. Не существует команд с одинаковыми левыми частями, т. е. если про- грамма машины T содержит выражения qi ai ® a j D q j и qt at ® ak D qk , то qi ¹ qt или ai ¹ at и D О {П, Л, Н } . Совокупность всех команд называется программой машины Тьюринга. Максимальное число команд в программе равно (n + 1) Ч m , где n + 1 = A и m + 1 = Q . Считается, что заключительное состояние команды q0 может стоять только в правой части команды, начальное состояние q1 может стоять как в левой так и в правой части команды. Выполнение одной команды называется шагом. Вычисление (или ра- бота) машины Тьюринга является последовательностью шагов одного за другим без пропусков, начиная с первого. Итак, МТ задана, если известны четыре конечных множества: внешний алфавит A , внутренний алфавит Q , множество D перемещений головки и программа машины, представляющая собой конечное множество команд. 9 § 2. Работа машины Тьюринга Работа машины полностью определяется заданием в первый (на- чальный) момент: 1) слова на ленте, т. е. последовательности символов, записанных в клетках ленты (слово получается чтением этих символов по клеткам ленты слева направо); 2) положения головки; 3) внутреннего со- стояния машины. Совокупность этих трех условий (в данный момент) на- зывается конфигурацией (в данный момент). Обычно в начальный момент внутренним состоянием машины является q1 , а головка находится либо над первой слева, либо над первой справа клеткой ленты. Заданное слово на ленте с начальным состоянием q1 и положение головки над первым словом называется начальной конфигурацией. В про- тивном случае говорят, что машина Тьюринга не применима к слову на- чальной конфигурации. Другими словами, в начальный момент конфигурация представима в следующем виде: на ленте, состоящей из некоторого числа клеток, в каж- дой клетке записан один из символов внешнего алфавита A , головка нахо- дится над первой слева или первой справа клеткой ленты и внутренним со- стоянием машины является q1 . Получившееся в результате реализации этой команды слово на ленте и положение головки называется заключи- тельной конфигурацией. Например, если в начальный момент на ленте записано слово a1La 2 a1a1 , то начальная конфигурация будет иметь вид: a1 a2 L a1 a1 q1 (под клеткой, над которой находится головка, указывается внутреннее со- стояние машины). 10

Наверное, сегодня не такого человека, который хотя бы раз не слышал о таком понятии, как тест Алана Тьюринга. Вероятно, большинство, в общем, далеко от понимания, что собой представляет такая система тестирования. Потому остановимся на ней несколько подробнее.

Что такое тест Тьюринга: основная концепция

Еще в конце 40-х годов прошлого столетия очень многие ученые умы занимались проблемами первых компьютерных разработок. Именно тогда один из членов некой негосударственной группы Ratio Club, занимавшейся исследованиями в области кибернетики, задался совершенно логичным вопросом: можно ли создать машину, которая бы думала, как человек, или, по крайней мере, имитировала его поведение?

Нужно ли говорить, кто придумал тест Тьюринга? По всей видимости, нет. За первоначальную основу всей концепции, которая и сейчас актуальна, был взят следующий принцип: сможет ли человек в течение некоторого времени общения с неким невидимым собеседником на совершенно разные произвольные темы определить, кто перед ним - реальный человек или машина? Иными словами, вопрос заключается не только в том, чтобы сымитировать машиной поведение реального человека, но и выяснить, может ли она думать самостоятельно. до сих пор этот вопрос остается спорным.

История создания

Вообще, если рассматривать тест Тьюринга как некую эмпирическую систему определения «человеческих» возможностей компьютера, стоит сказать, что косвенной основой для его создания послужили любопытные высказывания философа Альфреда Айера, которые он сформулировал еще в 1936 году.

Сам Айер сравнивал, так сказать, жизненный опыт разных людей, и на основе этого выразил мнение, что бездушная машина не сможет пройти ни один тест, поскольку мыслить не умеет. В лучшем случае это будет чистой воды имитация.

В принципе, так оно и есть. Для создания мыслящей машины одной имитации мало. Очень многие ученые в качестве примера приводят братьев Райт, которые построили первый самолет, отказавшись от тенденции имитировать птиц, которая, кстати сказать, была свойственна еще такому гению, как Леонардо да Винчи.

Истрия умалчивает, знал ли сам (1912-1954) об этих постулатах, тем не менее в 1950 году он составил целую систему вопросов, которая могла бы определить степень «очеловеченности» машины. И надо сказать, эта разработка и сейчас является одной из основополагающих, правда, уже при тестировании, например, компьютерных ботов и т. д. В реальности же принцип оказался таковы, что пройти тест Тьюринга удалось лишь нескольким программам. И то, «пройти» - сказано с большой натяжкой, поскольку результат тестирования никогда не имел показателя 100 процентов, в лучшем случае - чуть более 50.

В самом же начале своих исследований ученый использовал собственное изобретение. Оно получило название «тест-машина Тьюринга». Поскольку все беседы предполагалось ввести исключительно в печатном виде, ученый задал несколько основных директив по написанию ответов, таких как перемещение печатной ленты влево или вправо, печать определенного символа и т. д.

Программы ELIZA и PARRY

Со временем программы стали усложняться, а две из них в ситуациях, когда применялся тест Тьюринга, показали ошеломляющие на то время результаты. Таковыми стали ELIZA и PARRY.

Что касается «Элизы», созданной в 1960 году: исходя из вопроса, машина должна была определить ключевое слово и на его основе составить обратный ответ. Именно это позволяло обманывать реальных людей. Если такого слова не оказывалось, машина возвращала обобщенный ответ или повторяла один из предыдущих. Однако прохождение теста «Элизой» до сих пор остается под сомнением, поскольку реальных людей, которые общались с программой, изначально подготавливали психологически таким образом, чтобы они заранее думали, что разговаривают с человеком, а не с машиной.

Программа PARRY несколько похожа на «Элизу», но была создана для имитации общения параноика. Что самое интересное, для ее тестирования были использованы настоящие пациенты клиник. После записи стенограмм бесед в режиме телетайпа их оценивали профессиональные психиатры. Лишь в 48 процентах случаев они смогли правильно оценить, где человек, а где машина.

Кроме того, практически все тогдашние программы работали с учетом определенного промежутка времени, поскольку человек в те времена соображал намного быстрее машины. Сейчас - наоборот.

Суперкомпьютеры Deep Blue и Watson

Достаточно интересными выглядели разработки корпорации IBM, которые не то чтобы мыслили, но обладали невероятной вычислительной мощностью.

Наверное, многие помнят, как в 1997 году суперкомпьютер Deep Blue выиграл 6 партий в шахматы у тогдашнего действующего чемпиона мира Гарри Каспарова. Собственно, тест Тьюринга применим к этой машине весьма условно. Все дело в том, что в нее изначально было заложено множество шаблонов партий с невероятным количеством интерпретации развития событий. Машина могла оценивать порядка 200 миллионов позиций фигур на доске в секунду!

Компьютер Watson, состоявший из 360 процессоров и 90 серверов, выиграл американскую телевикторину, обойдя по всем параметрам двух других участников, за что, собственно, и получил 1 миллион долларов премии. Опять же, вопрос спорный, поскольку в машину были заложены невероятные объемы энциклопедических данных, а машина просто анализировала вопрос на предмет наличия ключевого слова, синонимов или обобщенных совпадений, после чего давала правильный ответ.

Эмулятор Eugene Goostman

Одним из самых интересных событий в этой области стала программа одессита Евгения Густмана и российского инженера Владимира Веселова, ныне проживающего в США, которая имитировала личность 13-летнего мальчика.

7 июня 2014 года программа Eugene показала свои возможности в полном объеме. Интересно, что в тестировании приняли участие 5 ботов и 30 реальных людей. Только в 33% случаев из ста жюри смогло определить, что это компьютер. Дело тут в том, что задача осложнялась тем, что у ребенка интеллект ниже, чем у взрослого человека, да и знаний поменьше.

Вопросы теста Тьюринга были самыми общими, правда, для Юджина (Euegene) были и некоторые конкретизированные вопросы о событиях в Одессе, которые не могли остаться незамеченными ни одним жителем. Но ответы все равно заставляли думать, что перед жюри ребенок. Так, например, на вопрос о местожительстве программа ответила сразу. Кода был задан вопрос, находился ли собеседник такого-то числа в городе, программа заявила, что не хочет об этом говорить. Когда собеседник попытался настаивать на разговоре в русле того, что именно произошло в этот день, Юджин открестился тем, что заявил, мол, вы и сами должны знать, чего ж его-то спрашивать? В общем, эмулятор ребенка оказался на редкость удачным.

Тем не менее это все-таки эмулятор, а не мыслящее существо. Так что восстание машин не состоится еще очень долго.

Обратная сторона медали

Напоследок остается добавить, что пока предпосылок для создания мыслящих машин в ближайшем будущем нет. Тем не менее если раньше вопросы распознавания относились именно к машинам, теперь то, что ты не машина, приходится доказывать практически каждому из нас. Посмотрите хотя бы на ввод капчи в Интернете для получения доступа к какому-то действию. Пока считается, что еще не создано ни одно электронное устройство, способное распознать искореженный текст или набор символов, кроме человека. Но кто знает, все возможно…